Принцип суперпозиции для потенциала электростатического поля в вакууме.

Рассмотрим электростатическое поле точечного неподвижного заряда. Это поле можно описать распределением в пространстве вектора напряженности электростатического поля. Вместе с тем, учитывая соотношения (1) раздела 2.4.1 и (1) раздела 2.4.7, для произвольной точки пространства запишем выражение для потенциала электростатического поля:

(1)

Здесь 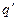- точечный электрический заряд, формирующий поле, 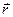- вектор, проведенный из точки расположения электрического заряда 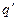в точку наблюдения. Произвольная постоянная выбрана равной нулю.

Если электростатическое поле образовано действием элементарного электрического заряда 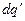, то соотношение (1) приобретает вид

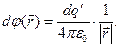(2)

Заметим, что смысл выражения «дифференциал 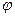» в формуле (2) и определении (1) раздела 2.4.5 различен. В выражении (2) речь идёт «о количестве», о части общей величины. В упомянутом определении речь идёт «о приращении» потенциала при переходе от точки пространства с радиус-вектором 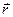к точке пространства с радиус-вектором .

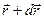Для потенциала электростатического поля справедлив принцип суперпозиции:

в рассматриваемой точке пространства потенциал электростатического поля, образованного суммой электрических зарядов, равен алгебраической сумме потенциалов электростатических полей, образованных каждым зарядом в отдельности.

В соответствии с принципом суперпозиции для потенциала электростатического поля имеют место следующие формулы:

для системы дискретных (сосредоточенных, точечных) зарядов

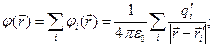(3)

для распределённых зарядов

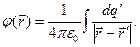(4)

В этих формулах штрихом отмечены координаты и величины электрических зарядов, образующих электростатическое поле, а вектор 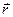является радиус-вектором точки наблюдения. Совокупности зарядов, распределенных по некоторому объёму с объёмной плотностью электрического заряда 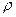, по поверхности с поверхностной плотностью электрического заряда 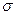или пространственной кривой с линейной плотностью электрического заряда 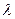, в соответствии с выражением (4) формируют электрические потенциалы:

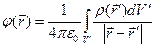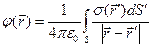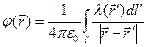, , . (5)

Приведенные соотношения особенно удобны при известных априори законах распределения объёмной плотности электрического заряда 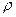, поверхностной плотности заряда 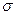и линейной (погонной) плотности заряда 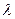: в этих случаях вычисление потенциала электростатического поля сводится к аналитическому или численному вычислению квадратур. Если распределение электрических зарядов заранее неизвестно, приведенные соотношения тоже не бесполезны, их можно использовать для получения интегральных уравнений, позволяющих найти обсуждаемые распределения зарядов по известным (или заданным) свойствам электростатического поля на границах рассматриваемой области пространства.

Вычисление квадратур (5) проще, чем вычисление соответствующих квадратур для векторов напряженности электростатического поля. Учитывая это обстоятельство, можно попытаться сначала вычислить распределение потенциала электростатического поля, а потом воспользоваться соотношением (4) раздела 2.4.5: вычисление частных производных проще вычисления интегралов. К сожалению, указанный приём «работает» только в том случае, когда удаётся получить замкнутую аналитическую формулу для распределения потенциала. В общем случае приходится иметь дело с выражением для потенциала в форме квадратуры.

В векторном анализе имеет место соотношение

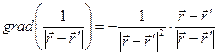. (6)

Если при вычислении градиента потенциала возможно вычисление частных производных под знаком определенного интеграла, то соотношение (6) позволяет убедиться, что фактически мы вернулись непосредственно к вычислению квадратур для напряженности электростатического поля (1)-(9) раздела 2.2.2.