Определение напряжённости электростатического поля по известному распределению потенциала.

Дифференциал потенциала электростатического поля вводят соотношением

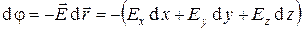. (1)

Легко видеть, что дифференциал потенциала 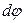равен элементарной работе против сил электростатического поля, совершаемой над единичным точечным зарядом на перемещении 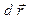. Здесь дифференциал потенциала 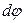не элементарная часть, а элементарное приращение, изменение потенциала при переходе от точки наблюдения 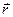к точке наблюдения .

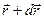Если в определении (1) учесть, что 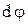- полный дифференциал, т.е.:

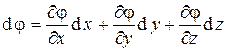, (2)

и сравнить соответствующие члены в формулах (1) и (2), то легко получить:

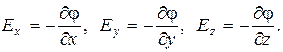(3)

В компактной форме записи формулы (3) имеют вид:

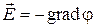, (4)

где вектор 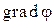в декартовой системе координат определен следующим образом

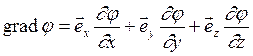. (5)

Градиент скалярного поля выделяет направление наискорейшего возрастания скалярной функции, а его модуль численно равен максимальной интенсивности возрастания этой функции в пересчёте на единицу длины.

В математическом анализе доказано интегральное соотношение

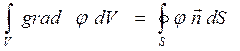, (6)

и справедливо символическое или абсолютное (независимое от выбора конкретной системы координат) определение градиента скалярной функции:

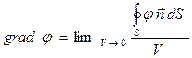. (7)

В этом случае можно предложить интуитивное определение градиента скалярной функции: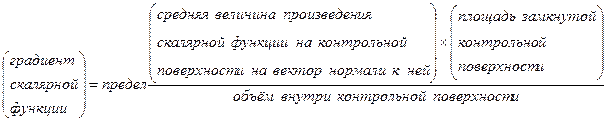

при стремлении к нулю объёма внутри контрольной поверхности. Это определение можно использовать для вычисления физических компонент градиента скалярной функции в криволинейных ортогональных системах координат.

В цилиндрической системе координат ( 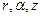) выражение для градиента скалярной функции имеет вид:

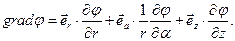(8)

В сферической системе координат 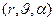выражение для градиента скалярной функции оказывается другим:

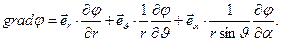(9)

Векторы 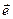с нижними индексами в этих выражениях являются ортами соответствующих координатных направлений.