Бесконечный круговой проводящий цилиндр в однородном поперечном электростатическом поле постоянной напряжённости.

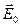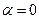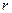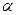Пусть цилиндрическая система координат выбрана таким образом, что продольная ось z совпадает с осью симметрии цилиндра, а направление вектора напряжённости внешнего (исходного) поля совпадает с направлением . Пусть радиус окружности поперечного сечения цилиндра равен а, положение в пространстве точки наблюдения М описывается полярными координатами и , значение продольной осевой координаты z безразлично. Рассматриваемая схема приведена на рис. 1. Электростатическое поле, возникающее в окрестности проводящего цилиндра, можно описать с помощью потенциала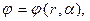 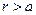, который удовлетворяет двумерному уравнению Лапласа в полярных координатах для произвольной точки наблюдения М и обращается в нуль на поверхности проводящего цилиндра 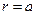. Так же как в предыдущем случае, потенциал результирующего поля будем искать как сумму потенциала однородного поля и потенциала индуцированного поля:

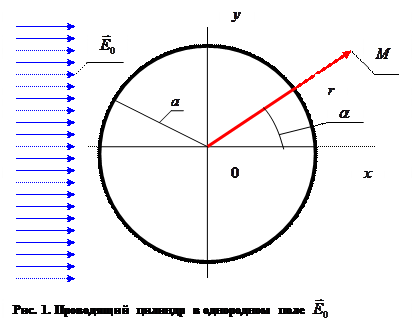
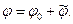(1)

Потенциал однородного исходного поля с учетом ориентации вектора напряженности электростатического поля и выбора направлений осей координат запишем виде:

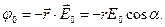(2)

Легко убедиться в том, что

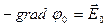и 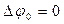в любой точке пространства.

Потенциал индуцированного поля 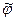должен удовлетворять уравнению Лапласа, исчезать при больших значениях координаты 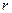и быть пропорциональным величине напряженности исходного поля. В случае проводящего шара к успеху привело предположение, что потенциал индуцированного поля можно построить как величину скалярного произведения вектора напряжённости исходного поля на градиент фундаментального решения 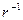уравнения Лапласа для бесконечного пространства. В условиях осевой симметрии фундаментальным решением уравнения Лапласа для безграничного пространства является функция 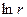. Ищем потенциал индуцированного поля в форме:

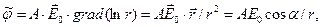(3)

где А – произвольная постоянная. Проверим непосредственным вычислением, что это выражение удовлетворяет уравнению Лапласа:

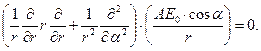(4)

Итак, потенциал результирующего поля можно записать в форме:

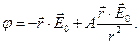(5)

Потребуем обращения в нуль этого выражения на поверхности проводящего цилиндра 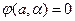. Постоянная A должна быть выбрана равной величине 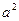. Окончательный результат построения зависимости потенциала результирующего поля от пространственных переменных имеет вид:

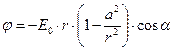. (6)

Располагая зависимостью для потенциала результирующего электростатического поля, вычислим вектор напряжённости результирующего поля:

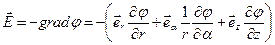. (7)

Физические компоненты вектора напряжённости результирующего электростатического поля определяются соотношениями:

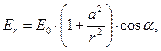
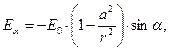
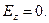(8)

Легко видеть, что на боковой поверхности проводящего цилиндра 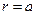касательные компоненты вектора напряжённости электростатического поля обращаются в нуль, а радиальная компонента 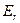определяет величину поверхностной плотности индуцированного электрического заряда:

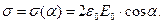(9)

Суммарная величина индуцированного электрического заряда на единице длины поверхности проводящего цилиндра равна нулю:

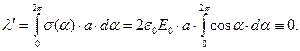(10)

Для полученного распределения поверхностной плотности индуцированного электрического заряда можно рассчитать отличную от нуля величину и направление дипольного электрического момента, приходящегося на единицу длины цилиндра.

Зависимости для радиальной и азимутальной физических составляющих вектора напряжённости электростатического поля позволяют записать дифференциальное уравнение соответствующих силовых линий:

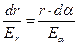
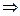
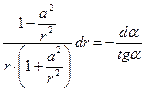. (11)

Общее решение этого уравнения

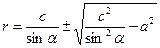(12)

при соответствующем выборе множества допустимых значений величины с описывает семейство силовых линий рассматриваемого электростатического поля.

Семейство эквипотенциальных поверхностей в соответствии с зависимостью (6) описывается уравнением:

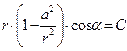
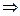
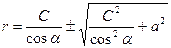(13)

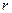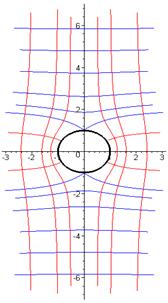
Физический смысл имеют результаты, обеспечивающие не только положительное значение величины , но и выполнение условия 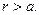На рис. 1 показано расположение семейства силовых линий вектора напряжённости и расположение семейства эквипотенциальных поверхностей электростатического поля, образованного проводящим цилиндром, который помещен в однородное поперечное электростатическое поле (напряжённость внешнего поля на рис. 1 параллельна оси х декартовой системы координат).

В рассматриваемом случае легко показать, что силовые линии перпендикулярны эквипотенциальным поверхностям. Действительно, из соотношения (11) получаем для силовых линий

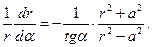(14)

Переходя к дифференциалам в определении эквипотенциальной поверхности (13), получаем

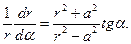(15)

при перемножении этих выражений получаем в правой части значение «минус единица», что подтверждает отмеченное выше свойство силовых линий и эквипотенциальных поверхностей.