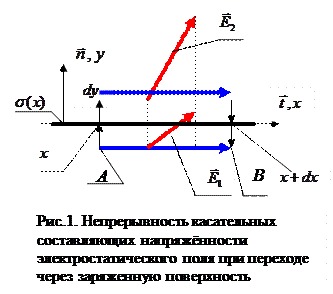
Непрерывность касательных составляющих напряжённости электростатического поля при переходе через заряженную поверхность.

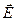Компоненты вектора напряжённости электростатического поля по разные стороны от заряженной поверхности связаны между собой двумя условиями. Одно из них в частных случаях было обнаружено при использовании принципа суперпозиции для расчёта векторов напряжённости полей, образованных заряженными поверхностями. В общем случае условие конечного скачка нормальной составляющей вектора напряжённости электрического поля при переходе через заряженную поверхность является следствием теоремы Гаусса для вектора 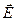в вакууме. Оказывается, что обязательное условие потенциальности электростатического поля приводит к требованию непрерывности касательных компонент напряжённости электростатического поля при переходе через заряженную поверхность

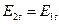, (1)

где индексом 2 отмечены величины полупространства «над поверхностью», в это полупространство направлена нормаль 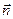к поверхности, а индексом 1 - величины «под поверхностью» (рис. 1). Индекс t указывает на то, что рассматриваются касательные составляющие вектора 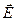. Заметим, что единичный вектор касательного направления 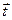в данной точке поверхности можно провести произвольно, а малую окрестность около рассматриваемой точки поверхности можно рассматривать как плоскую поверхность. Пусть ось х будет направлена вдоль касательного направления, а ось у – вдоль нормального направления к поверхности, на которой расположен электрический заряд с поверхностной плотностью .

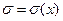Поскольку электростатическое поле является потенциальным, работа сил поля по перемещению положительного единичного точечного заряда из точки А в точку В, расположение которых показано на рис. 1, не зависит от формы траектории перемещения заряда. Если первая траектория расположена в нижнем полупространстве, рассматриваемая работа описывается выражением 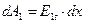. Вторая возможность состоит в переходе в верхнее полупространство, в смещении вдоль касательного направления на расстояние dx и в обратном переходе через поверхность в нижнее полупространство. Для упрощения выкладок положим, что смещение «вверх» состоит из двух одинаковых отрезков dy, один из которых расположен в нижнем, а второй – в верхнем полупространстве. Работа по перемещению положительного единичного точечного заряда по второй траектории равна

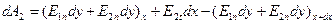. (2)

Воспользуемся известным соотношением для скачка величины нормальных составляющих вектора 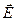при переходе через заряженную поверхность 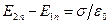и перепишем полученное выражение для элементарной работы dA₂: 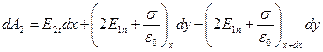. (3)

Предполагая непрерывное изменение вдоль координаты х заключённых в круглые скобки величин, получим:

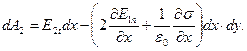(4)

Второе слагаемое в правой части полученного выражения является величиной второго порядка малости по сравнению с первым слагаемым, поэтому вторым слагаемым можно пренебречь. Эта оценка верна, если поверхностная плотность электрического заряда не меняется скачком в окрестности рассматриваемой точки поверхности и объёмная плотность электрического заряда выше и ниже заряженной поверхности в окрестности рассматриваемой точки поверхности не обращается в бесконечно большую величину. Во всех остальных случаях, практически в большинстве случаев, из соотношения 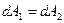следует условие

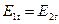(5).

Требование непрерывности касательных компонент напряжённости электростатического поля при переходе через заряженную поверхность является следствием потенциальности электростатического поля.

2.4.4. Локальное условие потенциальности электростатического поля. Заметим, что условие (4) раздела 2.4.2. будет выполнено, если дифференциальная форма Пфаффа 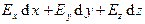является полным дифференциалом. В математическом анализе доказывают, что последнее влечет за собой необходимость выполнения совокупности условий:

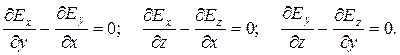(1)

Условия (1) являются дифференциальными (локальными) условиями потенциальности векторного поля 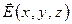в точке пространства (x,y,z). Векторное поле 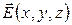является потенциальным в области, если условия (1) выполнены в каждой точке этой области.

Условия (1) можно компактно записать в векторной форме, если ввести в рассмотрение вектор «ротор» (или «вихрь») напряженности электрического поля :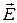

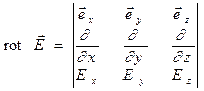, (2)

где 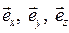- орты декартовой системы координат, определитель в определении (2) раскрывается по обычному правилу с тем условием, что дифференциальные операторы не должны стоять после функций 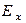, , 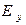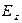. В иностранной литературе встречается обозначение ротора векторного поля .

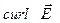С использованием определения (2) локальное (дифференциальное)

условие потенциальности электростатического поля имеет вид:

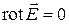. (3)

Внутренняя связь условий (4) раздела 2.4.2 и (3) настоящего раздела проявляется при рассмотрении математической теоремы Стокса:

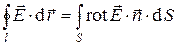, (4)

где 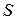- произвольная гладкая поверхность, натянутая на контур 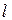, а направление нормали 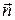к элементу площади поверхности 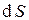выбрано так, чтобы при рассмотрении обхода контура из точки «конец вектора 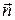» обход контура 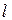осуществлялся против часовой стрелки.

Если левая часть соотношения (4) равна нулю (для произвольной поверхности S, ограниченной контуром 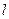), это эквивалентно условию (3).

Заметим, что теорема Стокса (4) служит основой для формального определения компонент вектора 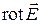безотносительно к выбору системы координат:

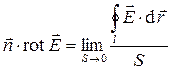. (5)

Соотношением (5) определяется математический смысл понятия (2). Более удобное математическое соотношение (теорема Грина) связывает между собой интеграл по объёму от ротора произвольного вектора и интеграл по замкнутой поверхности, ограничивающей этот объём, от векторного произведения нормали к элементу поверхности на рассматриваемый вектор:

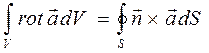. (6)

Из этого соотношение вытекает определение ротора вектора:

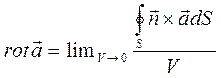. (7)

Перепишем числитель дроби в эквивалентной форме

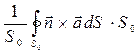. (8)

Теперь можно сформулировать интуитивное определение ротора вектора

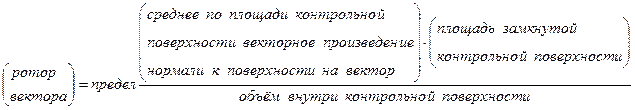при стремлении к нулю объёма внутри контрольной поверхности. Это определение можно использовать для расчета физических компонент ротора произвольного векторного поля в ортогональных криволинейных системах координат. Так в цилиндрической системе координат ( 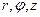) физические составляющие ротора вектора 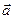можно получить, раскрывая определитель

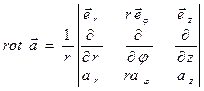. (9)

Выражение для ротора вектора 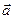в сферической системе координат ( 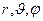) имеет вид:

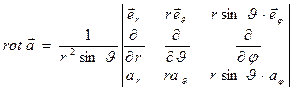. (10)

О правилах раскрытия подобных определителей было сказано выше. Векторное поле, ротор которого отличен от нуля, называют «вихревым» полем.