Потенциальность поля центральных сил.
Потенциал электростатического поля.
Электростатическое поле, создаваемое системой неподвижных электрических зарядов, обладает свойством потенциальности: работа сил электростатического поля по перемещению постоянного точечного заряда вдоль замкнутого контура равна нулю. Равносильное утверждение гласит: работа сил электростатического поля по перемещению постоянного точечного заряда из одной фиксированной точки пространства в другую не зависит от формы траектории, т.е. эта работа равна одной и той же величине для любых двух сравниваемых траекторий. Помимо важного теоретического значения рассматриваемого свойства, можно отметить и практическую его полезность: при расчёте величины работы по перемещению постоянного сосредоточенного заряда из одной точки пространства в другую можно выбирать траекторию движения, удобную для получения результата.
Потенциальность поля центральных сил.
Рассмотрим электростатическое поле одиночного точечного электрического заряда 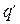 , помещенного в начало декартовой системы координат:
, помещенного в начало декартовой системы координат:
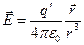 , (1)
, (1)
где 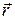 - радиус-вектор точки наблюдения,
- радиус-вектор точки наблюдения, 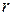 - модуль вектора
- модуль вектора 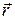 . Если в точке наблюдения помещен точечный заряд
. Если в точке наблюдения помещен точечный заряд 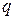 , то по определению понятия “напряженность электростатического поля” имеем
, то по определению понятия “напряженность электростатического поля” имеем
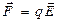 , (2)
, (2)
где 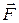 - сила, действующая на точечный заряд
- сила, действующая на точечный заряд 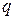 со стороны электростатического поля
со стороны электростатического поля 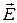 . Располагая зависимостью (2), легко написать выражение для элементарной работы
. Располагая зависимостью (2), легко написать выражение для элементарной работы 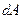 по бесконечно медленному перемещению заряда
по бесконечно медленному перемещению заряда 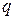 из точки, описываемой вектором
из точки, описываемой вектором 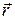 в соседнюю точку, описываемую вектором
в соседнюю точку, описываемую вектором 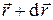 :
:
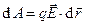 . (3)
. (3)
Элементарное смещение 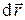 заряда
заряда 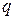 можно разложить на составляющую
можно разложить на составляющую 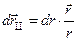 , параллельную вектору
, параллельную вектору 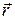 , и на составляющую
, и на составляющую 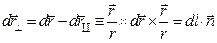 , перпендикулярную вектору
, перпендикулярную вектору 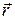 , она лежит в плоскости, в которой лежат векторы
, она лежит в плоскости, в которой лежат векторы 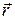 и
и 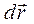 (рис. 1):
(рис. 1):
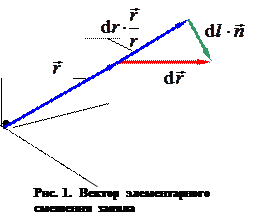
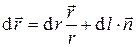 . (4)
. (4)
Здесь 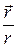 - орт направления вдоль
- орт направления вдоль 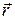 ,
, 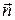 - орт направления, перпендикулярного направлению
- орт направления, перпендикулярного направлению 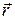 . По построению скалярное произведение вектора
. По построению скалярное произведение вектора 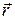 на орт
на орт 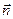 равно нулю (
равно нулю ( 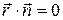 ). В этом случае элементарная работа сил поля по перемещению заряда
). В этом случае элементарная работа сил поля по перемещению заряда 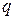 с учетом соотношений (1)-(4) описывается выражением:
с учетом соотношений (1)-(4) описывается выражением:
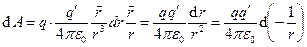 . (5)
. (5)
При перемещении постоянного точечного заряда 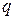 из положения 1 в положение 2 имеем
из положения 1 в положение 2 имеем
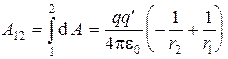 . (6)
. (6)
Здесь 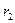 и
и 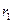 - расстояния (абсолютные величины) конечной и начальной точек траектории от точки расположения сосредоточенного электрического заряда
- расстояния (абсолютные величины) конечной и начальной точек траектории от точки расположения сосредоточенного электрического заряда 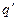 . Величина
. Величина 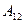 не зависит от формы траектории перемещения электрического заряда
не зависит от формы траектории перемещения электрического заряда 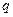 . Если перемещение заряда заканчивается в исходной точке, то, очевидно,
. Если перемещение заряда заканчивается в исходной точке, то, очевидно, 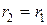 и мы получаем
и мы получаем
 , (7)
, (7)
где индексом “0” помечено, что перемещение осуществлялось по замкнутому контуру. Результат (7) позволяет более наглядно убедиться в том, что работа по перемещению заряда 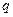 из первого положения во второе не зависит от формы траектории для рассматриваемого случая.
из первого положения во второе не зависит от формы траектории для рассматриваемого случая.
 Допустим, что заряд
Допустим, что заряд 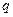 переместили по одной траектории из положения 1 в положение 2 , а затем по другой траектории вернули в положение 1 (рис.2). Суммарная работа в описанном процессе равна нулю. Это означает, что работа по первой траектории перемещения 1->2 равна работе перемещения 2->1 по второй траектории с обратным знаком. Очевидно, что работа перемещения 1->2 и работа перемещения 2->1 по одной и той же траектории равны по величине и противоположны по знаку. Отсюда с необходимостью следует, что работа перемещения электрического заряда 1->2 по первой или по второй траектории совпадают между собой.
переместили по одной траектории из положения 1 в положение 2 , а затем по другой траектории вернули в положение 1 (рис.2). Суммарная работа в описанном процессе равна нулю. Это означает, что работа по первой траектории перемещения 1->2 равна работе перемещения 2->1 по второй траектории с обратным знаком. Очевидно, что работа перемещения 1->2 и работа перемещения 2->1 по одной и той же траектории равны по величине и противоположны по знаку. Отсюда с необходимостью следует, что работа перемещения электрического заряда 1->2 по первой или по второй траектории совпадают между собой.
Поскольку электростатическое поле в общем случае образовано системой неподвижных элементарных, практически «точечных зарядов», для каждого из них соотношение (7) справедливо и справедлив принцип суперпозиции для вектора напряжённости электростатического поля, то можно утверждать, что описанным выше свойством потенциальности обладает произвольное электростатическое поле.
Следствием потенциальности произвольного электростатического поля является возможность введения понятия «потенциальная энергия U электрического заряда q в рассматриваемой точке пространства, в котором имеет место электростатическое поле», при этом работа по перемещению электрического заряда из одной точки пространства в другую равна разности соответствующих значений потенциальной энергии, взятой с обратным знаком.
Дата добавления: 2017-09-01; просмотров: 1975;











