Формулы Френеля (классическая электродинамика).
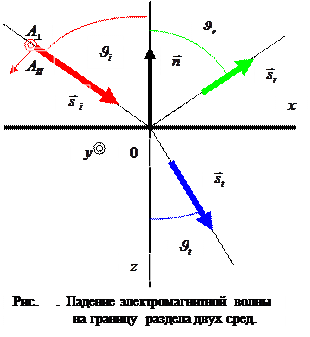 Рассмотрим падение плоской гармонической электромагнитной волны на границу раздела двух однородных изотропных непроводящих сред (рис. ). Нормаль к поверхности раздела определена вектором
Рассмотрим падение плоской гармонической электромагнитной волны на границу раздела двух однородных изотропных непроводящих сред (рис. ). Нормаль к поверхности раздела определена вектором  , углы между нормалью и направлениями распространения падающей, отражённой и преломлённой волн обозначены символом
, углы между нормалью и направлениями распространения падающей, отражённой и преломлённой волн обозначены символом  с подстрочным индексом
с подстрочным индексом 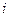 ,
,  или
или 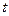 соответственно. Направления распространения описанных плоских волн заданы единичными ортами
соответственно. Направления распространения описанных плоских волн заданы единичными ортами 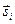 ,
, 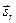 и
и 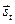 . Вектор
. Вектор 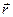 в последующих выкладках является радиус-вектором точки наблюдения, а величины
в последующих выкладках является радиус-вектором точки наблюдения, а величины 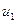 и
и 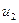 - это фазовые скорости распространения волны в первой (падающая и отражённая волна) и во второй (преломлённая волна) среде. Полагаем, что плоскость поляризации электромагнитной волны является плоскостью колебаний вектора напряжённости электрического поля. Электромагнитную волну с произвольной ориентацией плоскости поляризации представляем в виде суперпозиции двух волн - волны с плоскостью поляризации, параллельной плоскости падения, и волны с плоскостью поляризации, перпендикулярной плоскости падения. Таким образом, получаем соотношение:
- это фазовые скорости распространения волны в первой (падающая и отражённая волна) и во второй (преломлённая волна) среде. Полагаем, что плоскость поляризации электромагнитной волны является плоскостью колебаний вектора напряжённости электрического поля. Электромагнитную волну с произвольной ориентацией плоскости поляризации представляем в виде суперпозиции двух волн - волны с плоскостью поляризации, параллельной плоскости падения, и волны с плоскостью поляризации, перпендикулярной плоскости падения. Таким образом, получаем соотношение:
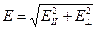 . (1)
. (1)
Если амплитуды колебаний вектора напряжённости электрического поля 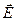 падающей волны равны соответственно
падающей волны равны соответственно  и
и  для той или иной ориентации плоскости поляризации, то имеют мест соотношения:
для той или иной ориентации плоскости поляризации, то имеют мест соотношения:
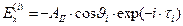 ,
, 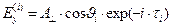 ,
, 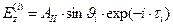 , (2)
, (2)
 . (3)
. (3)
Эти отношения справедливы для выбранных положительных направлений векторов 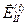 и
и 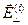 , показанных на рис. (ось
, показанных на рис. (ось 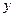 перпендикулярна плоскости рисунка и направлена «на нас», вектор
перпендикулярна плоскости рисунка и направлена «на нас», вектор  направлен по оси
направлен по оси 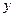 ).
).
Для вектора напряжённости магнитного поля в падающей волне воспользуемся полученными ранее результатами:
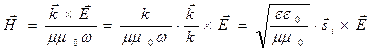 . (4)
. (4)
В соотношении (4) вектор  - волновой вектор (
- волновой вектор ( 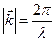 , где
, где 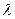 - длина волны). В соответствии с результатом (4) запишем координатное представление вектора напряжённости магнитного поля падающей волны:
- длина волны). В соответствии с результатом (4) запишем координатное представление вектора напряжённости магнитного поля падающей волны:
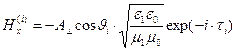 ,
,
 , (5)
, (5)
 .
.
Пусть 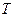 - комплексная амплитуда преломлённой волны, при этом
- комплексная амплитуда преломлённой волны, при этом 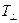 направлена «на нас» вдоль оси
направлена «на нас» вдоль оси 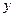 , а
, а 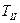 перпендикулярна вектору
перпендикулярна вектору 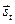 и направлена в сторону оси
и направлена в сторону оси  . Описанные ориентации амплитуд условно принимаются положительными. Для составляющих электромагнитного поля в преломлённой волне, также как и в падающей волне, получаем зависимости:
. Описанные ориентации амплитуд условно принимаются положительными. Для составляющих электромагнитного поля в преломлённой волне, также как и в падающей волне, получаем зависимости:
 ,
, 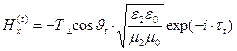 ,
,
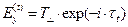 ,
, 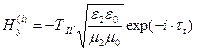 , (6)
, (6)
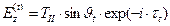 ,
,  .
.
В выражениях (6) мгновенная фаза гармонических колебаний  имеет вид:
имеет вид:
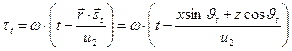 . (7)
. (7)
Продолжим описание взаимодействия плоской волны с границей раздела сред. Пусть 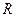 - комплексная амплитуда отражённой волны, при этом
- комплексная амплитуда отражённой волны, при этом 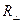 направлена «на нас» вдоль оси
направлена «на нас» вдоль оси 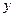 , а
, а 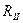 перпендикулярна вектору
перпендикулярна вектору 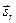 и направлена в сторону оси
и направлена в сторону оси 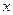 . Описанные ориентации амплитуд условно принимаются положительными. Для составляющих электромагнитного поля в отражённой волне, также как и в падающей волне, получаем зависимости:
. Описанные ориентации амплитуд условно принимаются положительными. Для составляющих электромагнитного поля в отражённой волне, также как и в падающей волне, получаем зависимости:
 ,
, 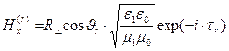 ,
,
 ,
, 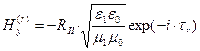 , (8)
, (8)
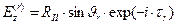 ,
, 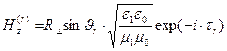 .
.
Для отражённой волны мгновенная фаза гармонических колебаний 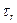 имеет вид:
имеет вид:
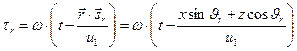 . (9)
. (9)
Выписанные выше выражения для мгновенных значений координатных составляющих электромагнитного поля справедливы в любой точке плоскости падения и в любой момент времени.
В соответствии с общими интегральными теоремами электродинамики на границе раздела двух сред (  - координата радиус-вектора
- координата радиус-вектора 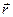 точки наблюдения равна нулю) в любой момент времени
точки наблюдения равна нулю) в любой момент времени 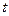 должны выполняться условия непрерывности касательных компонент вектора напряжённости электрического поля
должны выполняться условия непрерывности касательных компонент вектора напряжённости электрического поля 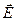 и касательных компонент напряжённости магнитного поля
и касательных компонент напряжённости магнитного поля  . Последнее условие справедливо, если на поверхности раздела сред отсутствует поверхностная плотность тока проводимости.
. Последнее условие справедливо, если на поверхности раздела сред отсутствует поверхностная плотность тока проводимости.
Итак, при z=0 требуем выполнения условий:
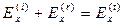 ,
, 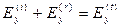 , (10)
, (10)
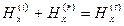 ,
, 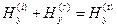 . (11)
. (11)
Обеспечить выполнение условий (10)-(11) в произвольный момент времени можно только, если потребовать выполнения равенства экспоненциальных множителей в выражениях для компонент векторов 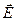 и
и  на границе раздела. Приравнивая друг другу выражения
на границе раздела. Приравнивая друг другу выражения 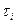 и
и 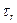 при z=0, убеждаемся, что угол падения равен углу отражения:
при z=0, убеждаемся, что угол падения равен углу отражения: 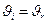 . Приравнивая друг другу выражения
. Приравнивая друг другу выражения 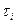 и
и  при z=0, убеждаемся, что справедлив закон синусов Снеллиуса: синус угла падения относится к синусу угла преломления как фазовая скорость падающей волны к фазовой скорости преломлённой волны (или как показатель преломления второй среды относится к показателю преломления первой среды). Ранее описанный приём был использован безотносительно к природе плоской волны (раздел ). Ниже будем пользоваться установленными результатами.
при z=0, убеждаемся, что справедлив закон синусов Снеллиуса: синус угла падения относится к синусу угла преломления как фазовая скорость падающей волны к фазовой скорости преломлённой волны (или как показатель преломления второй среды относится к показателю преломления первой среды). Ранее описанный приём был использован безотносительно к природе плоской волны (раздел ). Ниже будем пользоваться установленными результатами.
Четыре уравнения (10)-(11) распадаются на две независимые системы:
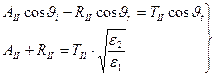 (12)
(12)
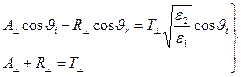 (13)
(13)
Факт расщепления условий сопряжения электромагнитного поля на границе раздела сред на две независимые системы уравнений служит обоснованием гипотезы Френеля о возможности рассматривать по отдельности явления отражения и преломления световых волн, колебания в которых параллельны или перпендикулярны плоскости падения волны.
Уравнения (12)-(13) записаны с использованием приближения 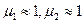 , при этом
, при этом  ,
, 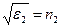 . Осталось только решить системы уравнений (12) и (13). После несложных выкладок с использованием известных соотношений между тригонометрическими функциями получаем результаты:
. Осталось только решить системы уравнений (12) и (13). После несложных выкладок с использованием известных соотношений между тригонометрическими функциями получаем результаты:
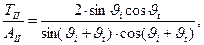
 (14)
(14)
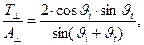
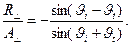 (15)
(15)
Для удобства практических расчётов приведём решения систем уравнений (12)-(13) с использованием понятия показатель преломления:

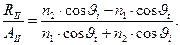 (16)
(16)

 (17) Соотношения (14) и (15) позволяют получить соответствующие выражения и для компонент напряжённости магнитного поля, при желании читатель имеет возможность эти выкладки проделать самостоятельно.
(17) Соотношения (14) и (15) позволяют получить соответствующие выражения и для компонент напряжённости магнитного поля, при желании читатель имеет возможность эти выкладки проделать самостоятельно.
Соотношения (14)-(15) полностью решают рассматриваемую проблему. Они получены с использованием условий непрерывности касательных составляющих векторов напряжённости электрического и магнитного полей на границе раздела двух сред (10)-(11). Но из интегральных теорем классической электродинамики следуют определённые условия, которым должны удовлетворять нормальные к границе раздела составляющие тех же векторных полей:
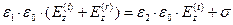 , (18)
, (18)
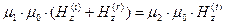 . (19)
. (19)
В условии (18) величина  - это поверхностная плотность свободных электрических зарядов. Если в уравнение (18) подставить полученные выше решения и воспользоваться приближением исчезающее малого отличия магнитной проницаемости сред от единицы,
- это поверхностная плотность свободных электрических зарядов. Если в уравнение (18) подставить полученные выше решения и воспользоваться приближением исчезающее малого отличия магнитной проницаемости сред от единицы,
то получим с учётом второго из уравнений системы (12), которое выше использовалось для получения решения, что на поверхности раздела сред действительно не может быть отличной от нуля поверхностной плотности свободных электрических зарядов. А если в уравнение (19) подставить полученные выше решения, то с той же степень точности получаем второе из уравнений системы (13). Таким образом, можно считать доказанным, что нормальные компоненты векторов напряжённости электрического и магнитного поля
удовлетворяют условиям на границе раздела двух сред. Мы ещё раз имеем возможность убедиться в том, насколько внутренне строго организована электромагнитная волна.
Экспериментальная проверка формул Френеля основана на измерении отношения интенсивности отражённой волны к интенсивности падающей волны. Если падающий свет является естественным, осреднённые значения квадратов амплитуд колебаний  и
и  совпадают, при этом справедливо соотношение:
совпадают, при этом справедливо соотношение:
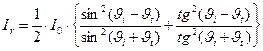 , (20)
, (20)
где 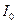 - интенсивность естественного падающего света,
- интенсивность естественного падающего света, 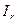 - интенсивность отражённого частично поляризованного света. Соотношение (20) многократно экспериментально проверялось, оно хорошо описывает экспериментальные результаты. Ради полноты обсуждения проблемы заметим, что в оптике известны случаи отклонения от формул Френеля, но связаны они не с основами электродинамики, а с тем, что выше рассматривалась идеализированная модель явления, упрощённо описывающая свойства поверхности раздела и, вообще говоря, динамические свойства материальных сред.
- интенсивность отражённого частично поляризованного света. Соотношение (20) многократно экспериментально проверялось, оно хорошо описывает экспериментальные результаты. Ради полноты обсуждения проблемы заметим, что в оптике известны случаи отклонения от формул Френеля, но связаны они не с основами электродинамики, а с тем, что выше рассматривалась идеализированная модель явления, упрощённо описывающая свойства поверхности раздела и, вообще говоря, динамические свойства материальных сред.
Сравнивая выражения (14) и (15) с «формулами Френеля», убеждаемся в их идентичности. Но в рамках классической электродинамики в отличие от теории Френеля не содержится внутренне противоречивых элементов, правда, – следует и об этом не забывать – к такому триумфу физики шли около 40 лет.
Наклонное падение плоской гармонической электромагнитной волны на границу раздела сред диэлектрик-проводник.
Целью настоящего раздела является описание явления отражения-преломления плоской однородной гармонической волны при её наклонном падении на плоскую границу раздела диэлектрической среды и проводящей среды. Необходимость вернуться к этому вопросу после рассмотрения формул Френеля для случая наклонного падения электромагнитной волны на границу раздела двух диэлектрических сред обусловлена некоторыми новыми специфическими закономерностями явления, которые возникают из-за того, что одна из сред является проводящей.
Переменное электромагнитное поле описывается системой уравнений Максвелла в дифференциальной форме, величины диэлектрической 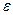 и магнитной
и магнитной  проницаемостей и удельной электропроводности
проницаемостей и удельной электропроводности  гипотетической (т.е. модельной) среды считаем независящими от времени и пространственных координат. В непроводящей среде (диэлектрик) выполняется условие
гипотетической (т.е. модельной) среды считаем независящими от времени и пространственных координат. В непроводящей среде (диэлектрик) выполняется условие 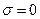 .
.
Решение системы уравнений Максвелла представляем в форме плоских гармонических бегущих волн:
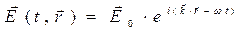 ,
, 
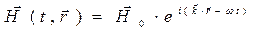 ,
, 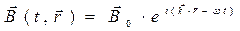 , (1)
, (1)
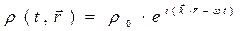
где 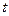 - текущее время,
- текущее время,  - круговая частота волны,
- круговая частота волны, 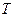 - период колебаний физической величины, принимающей участие в волновом процессе. Здесь
- период колебаний физической величины, принимающей участие в волновом процессе. Здесь 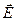 - вектор напряжённости электрического поля,
- вектор напряжённости электрического поля,  - вектор напряжённости магнитного поля,
- вектор напряжённости магнитного поля, 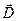 - вектор электрического смещения,
- вектор электрического смещения,  - вектор магнитной индукции,
- вектор магнитной индукции, 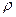 - объёмная плотность сторонних электрических зарядов. Предполагаем, как и прежде, что круговая частота
- объёмная плотность сторонних электрических зарядов. Предполагаем, как и прежде, что круговая частота 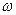 является вещественной постоянной скалярной величиной, а вектор
является вещественной постоянной скалярной величиной, а вектор 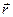 - радиус-вектором точки наблюдения. Волновой вектор ниже рассматриваем как вектор с комплексными компонентами:
- радиус-вектором точки наблюдения. Волновой вектор ниже рассматриваем как вектор с комплексными компонентами:
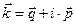 , (2)
, (2)
где отличные друг от друга по величине и направлению векторы 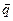 и
и 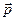 имеют вещественные компоненты.
имеют вещественные компоненты.
Векторные величины  в соотношении (1) будем считать постоянными векторными величинами (амплитудами плоских гармонических волн). Результаты вычисления дивергенции и ротора векторных величин (1) были не один раз описаны в предыдущих разделах. Таким образом, система уравнений переменного гармонического электромагнитного поля, записанная для векторов напряжённости электрического и магнитного полей, формально приобретает «алгебраический» вид:
в соотношении (1) будем считать постоянными векторными величинами (амплитудами плоских гармонических волн). Результаты вычисления дивергенции и ротора векторных величин (1) были не один раз описаны в предыдущих разделах. Таким образом, система уравнений переменного гармонического электромагнитного поля, записанная для векторов напряжённости электрического и магнитного полей, формально приобретает «алгебраический» вид:
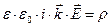 , (3)
, (3)
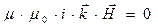 , (4)
, (4)
 , (5)
, (5)
 . (6)
. (6)
Из уравнений (5) и (6) следует, что должны быть выполнены условия «алгебраической ортогональности» векторов  и
и 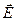 ,
,  и
и  и
и 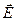 и
и  . Из уравнений (3) и (6) следует обращение в нуль объёмной плотности сторонних зарядов (
. Из уравнений (3) и (6) следует обращение в нуль объёмной плотности сторонних зарядов (  ).
).
Используя уравнение (5) как зависимость вектора напряжённости магнитного поля от вектора напряжённости электрического поля, из уравнения (6) получаем дисперсионное уравнение в форме:
 ,
,  ,
, 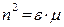 ,
, 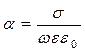 . (7)
. (7)
В дисперсионном уравнении (7) специально подчёркнут комплексный характер вектора  в проводящей среде, поскольку величина
в проводящей среде, поскольку величина 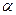 , пропорциональная проводимости среды, отлична от нуля. Разделяя действительную и мнимую части комплексного уравнения (7), получаем систему уравнений с действительными переменными:
, пропорциональная проводимости среды, отлична от нуля. Разделяя действительную и мнимую части комплексного уравнения (7), получаем систему уравнений с действительными переменными:
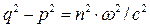 ,
, 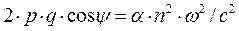 . (8)
. (8)
Угол 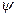 в системе уравнений (8) – угол между двумя действительными векторами
в системе уравнений (8) – угол между двумя действительными векторами 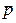 и
и 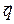 , величины p и q без стрелок над ними представляют собой модули соответствующих векторов. Решение системы уравнений (8), отвечающее физическому смыслу рассматриваемых величин, имеет вид:
, величины p и q без стрелок над ними представляют собой модули соответствующих векторов. Решение системы уравнений (8), отвечающее физическому смыслу рассматриваемых величин, имеет вид:
 ,
, 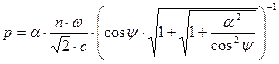 . (9)
. (9)
При необходимости в выражения (9) можно подставить параметры первой (непроводящей) или второй (проводящей) среды. В случае непроводящей среды параметр 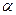 обращается в нуль, вместе с ним в нуль обращается и вектор
обращается в нуль, вместе с ним в нуль обращается и вектор 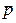 , волновой вектор
, волновой вектор  становится вектором с действительными компонентами.
становится вектором с действительными компонентами.

 Ниже рассматриваем падение электромагнитной волны из диэлектрика (среда 1) в проводник (среда 2). В диэлектрике величина
Ниже рассматриваем падение электромагнитной волны из диэлектрика (среда 1) в проводник (среда 2). В диэлектрике величина 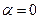 , поэтому волновой вектор
, поэтому волновой вектор  имеет только действительную составляющую, а его ориентация в пространстве определяется единственным образом – направлением вектора
имеет только действительную составляющую, а его ориентация в пространстве определяется единственным образом – направлением вектора  . Плоскость падения электромагнитной волны определяется вектором
. Плоскость падения электромагнитной волны определяется вектором 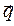 и нормалью к поверхности раздела, положительное направление нормали выбираем в сторону среды 2. Декартову систему координат удобно построить следующим образом. Ось z направим по направлению нормали, ось х расположим в плоскости падения, а ось у – перпендикулярно плоскости падения, причём направления соответствующих ортов
и нормалью к поверхности раздела, положительное направление нормали выбираем в сторону среды 2. Декартову систему координат удобно построить следующим образом. Ось z направим по направлению нормали, ось х расположим в плоскости падения, а ось у – перпендикулярно плоскости падения, причём направления соответствующих ортов 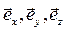 образуют правую систему координат.
образуют правую систему координат.
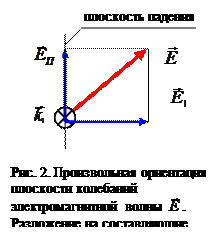
В линейной теории электромагнитного поля справедлив принцип суперпозиции. Это даёт нам право рассматривать по отдельности более простые случаи поляризации падающей электромагнитной волны. Рассмотрим рисунок 2. Пусть волновой вектор падающей волны перпендикулярен плоскости рисунка 2, вертикальная ось координат
лежит в плоскости падения, а горизонтальная ось перпендикулярна плоскости падения. Произвольный вектор 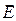 , перпендикулярный волновому вектору, можно разложить на две составляющие:
, перпендикулярный волновому вектору, можно разложить на две составляющие:  и
и 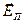 . Первую ориентацию плоскости колебаний электромагнитной волны называют S-поляризацией, вторую –P-поляризацией. Анализ S-поляризации электромагнитной волны несколько проще, чем анализ P-поляризации, поэтому сначала рассмотрим этот случай.
. Первую ориентацию плоскости колебаний электромагнитной волны называют S-поляризацией, вторую –P-поляризацией. Анализ S-поляризации электромагнитной волны несколько проще, чем анализ P-поляризации, поэтому сначала рассмотрим этот случай.
Дата добавления: 2017-09-01; просмотров: 2140;











