Классическая электронная теория дисперсии.

До сих пор мы рассматривали материальные среды, свойства которых оставались неизменными вне зависимости от того, распространяется ли или отсутствует в среде электромагнитная волна. В реальных условиях электромагнитная волна оказывает воздействие на материальную среду. Строгая современная теория этого взаимодействия основывается на представлениях квантовой статистической физики, изложение которой выходит за рамки настоящего пособия. В настоящем разделе обсудим классический вариант теории взаимодействия электромагнитной волны с электрическими зарядами частиц, входящих в состав атомов и молекул среды, предложенный почти сто лет тому назад Х.Лоренцем (Лоренц Хендрик Антон (1853-1928) – нидерландский физик-теоретик). Несмотря на упрощения, принятые в модели Лоренца, его теория позволила качественно, а во многих случаях и количественно объяснить особенности распространения электромагнитных волн в различных средах.

Первичная электромагнитная волна воздействует на электроны и ионы вещества, последние приобретают неравномерное движение, вследствие чего происходит излучение вторичных электромагнитных волн. В среде возникает суммарное электромагнитное поле. Ионы обладают значительно большей инерционностью по сравнению с лёгкими электронами, поэтому во многих случаях их можно считать неподвижными. Электроны в многоэлектронных атомах по-разному связаны с ионом, эта связь, в первом приближении «гармоническая»- отклонения от положения устойчивого равновесия малы, слабее для валентных электронов, расположенных на внешней электронной оболочке атома. Собственные частоты колебаний системы электрон-ион зависят от вида атома и номера электронной оболочки, к которой принадлежит атом. Вынужденные колебания заряженных частиц среды обуславливают такие явления как дисперсия, поглощение и рассеяние электромагнитной волны.

Теория Лоренца является локальной. Принимается, что в рассматриваемой точке пространства напряжённость электрического поля Е колеблется по гармоническому закону вдоль одного фиксированного направления х. Движение электрона происходит под действием «упругой» возвращающей силы, силы сопротивления, пропорциональной скорости электрона, и внешней гармонической силы электрического поля волны:

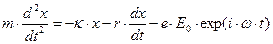. (67)

Здесь 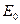- амплитуда напряжённости электрического поля, 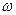- круговая частота электромагнитной волны. Сила сопротивления в уравнении (1) введена формально, таким образом предпринимается попытка как-то учесть, что в неравномерном движении электрон должен испускать энергию излучения. Силой Лоренца – воздействие магнитного поля волны на движение электрона – пренебрегаем. Перепишем уравнение (67):

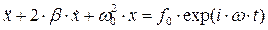. (68)

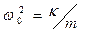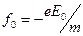В уравнении (68) использованы обозначения: - круговая частота собственных колебаний электрона, - коэффициент поглощения, - относительная амплитуда вынуждающей силы.

Рассматривая процесс установившихся колебаний, ищем решение уравнения (68) в форме

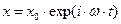(69)

и получаем для амплитуды вынужденных колебаний электрона уравнение:

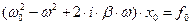. (70)

Решение уравнения (70) имеет вид:

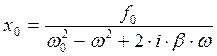. (71)

Искомая зависимость смещения электрона из положения равновесия с течением времени определяется выражением (69). Электрический дипольный момент электрона равен

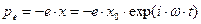. (72)

При выводе соотношения (72) молчаливо предполагалось, что на движение рассматриваемого электрона никак не влияет движение остальных электронов, следствием этого является предположение, что все электроны с частотой собственных колебаний 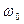движутся одинаково. В этом случае суммарный электрический момент единицы объёма среды будет равен произведению дипольного электрического момента электрона на количество электронов N в единице объёма:

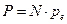. (73)

Вспоминая форму зависимости поляризованности среды от напряжённости электрического поля

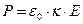, (74)

где 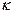- диэлектрическая восприимчивость среды, для параметра 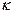получаем выражение:

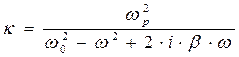. (75)

Здесь параметр свойств среды «плазменная частота» введена соотношением:

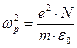. (76)

То обстоятельство, что величина 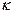оказалась комплексной величиной, свидетельствует о том, что фазы колебаний вектора напряженности электрического поля волны и вектора поляризованности среды не совпадают по фазе колебаний. Это явление имеет место, если параметр 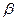отличен от нуля ( ).

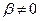Вычислим величину диэлектрической проницаемости среды:

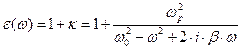. (77)

Здесь необходимо обратить внимание на два обстоятельства. Первое – это зависимость динамической диэлектрической проницаемости среды от круговой частоты электромагнитной волны, второе – диэлектрическая проницаемость является в общем случае комплексной величиной. Следствием второго обстоятельства является различие в значениях мгновенных фаз колебаний вектора напряжённости электрического поля и вектора электрической индукции 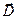. Более подробный анализ свойств электромагнитной волны в среде с комплексной диэлектрической проницаемостью обнаруживает и различие в фазах колебаний вектора напряжённости электрического поля и вектора напряжённости магнитного поля, что характерно для электропроводящих сред.

В тех случаях, когда поглощением электромагнитной энергии волны можно пренебречь, зависимость (77) переходит в соотношение Куросавы:

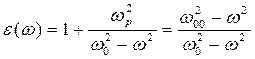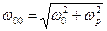, . (78)

Здесь явно выделено значение круговой частоты 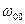, при которой величина диэлектрической проницаемости среды обращается в ноль. Если относительная магнитная проницаемость среды 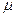равна единице, для квадрата величины показателя преломления среды можно записать зависимость:

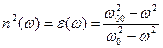. (79)

Разложим полученное выражение в ряд Тэйлора по чётным степеням круговой частоты в окрестности нуля с сохранением трёх первых членов:

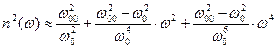. (80)

Для газов в области частот, прозрачной для электромагнитного излучения, величина 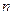настолько мало отличается от единицы, что выражение 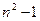можно приближённо заменить на выражение 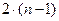, тогда с учётом зависимости 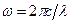для вакуума из соотношения (14) следует формула Коши (Огюстен Луи Коши (1789-1857) – французский математик):

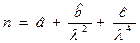, (81)

постоянные в которой ранее предлагалось подбирать экспериментально. В рассматриваемой теории эти постоянные определяются через физические свойства среды, что обосновывает справедливость полуэмпирической формулы Коши и позволяет теоретически рассчитать зависимость коэффициента преломления среды от длины волны.

Перейдём к рассмотрению «дисперсионных кривых» для распространения электромагнитных волн в прозрачных средах (среды без поглощения). Будем считать, что справедливо соотношение Куросавы в форме (79). Дисперсионное уравнение для рассматриваемого случая имеет вид: 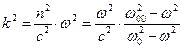. (82)

Для величины 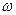имеет место биквадратное уравнение: 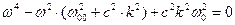, (83)

решением которого являются соотношения:

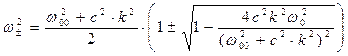. (84)

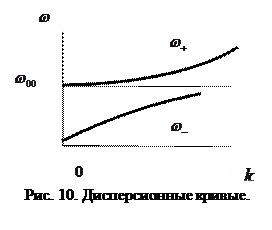
В соответствии с результатом (84) действительному волновому числу 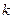соответствуют два действительных значения величины круговой частоты 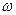. Говорят, что дисперсионная кривая (т.е. зависимость круговой частоты 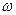от волнового числа 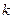) имеет две «ветви», характерный вид которых показан на рис. 10. В рассматриваемом случае в среде могут распространяться электромагнитные волны двух типов.

Для прозрачных сред (имеются в виду среды без поглощения) характерна зависимость относительной диэлектрической проницаемости среды от круговой частоты электромагнитной волны, показанная на рис. 11.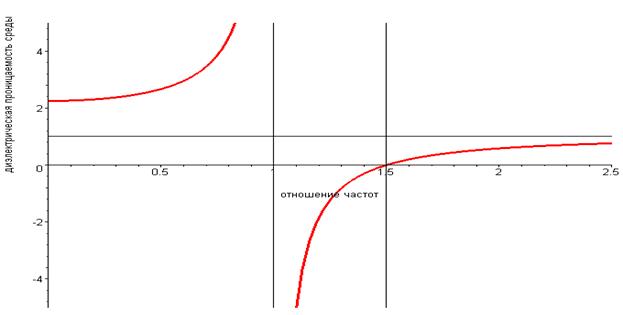

Рис. 11. Зависимость относительной диэлектрической проницаемости от относительной частоты электромагнитной волны.

На этом рисунке по вертикали отложены значения относительной диэлектрической проницаемости среды, а по горизонтали – отношение круговой частоты электромагнитной волны к собственной круговой частоте колебаний электронов 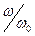. График построен для случая 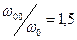, что соответствует отношению плазменной частоты к собственной частоте колебаний электронов 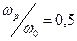. На рисунке имеется область отрицательных значений относительной диэлектрической проницаемости 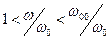. В этой области изменения частоты электромагнитной волны вектор электрического смещения колеблется в противофазе по отношению к колебанию вектора напряжённости электрического поля .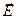

Показатель преломления прозрачной среды (его действительная часть!) тоже зависит от круговой частоты электромагнитной волны. Эта зависимость показана на рис. 12.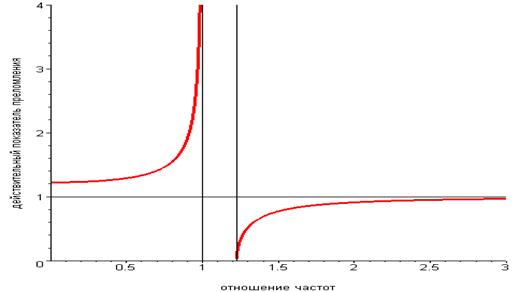

Рис. 12. Зависимость показателя преломления прозрачной среды от круговой частоты электромагнитной волны.

Значения физических параметров системы совпадают с параметрами предыдущего рисунка.

В реальных средах имеет место поглощение, иногда исчезающее малое, но отличное от нуля. Вакуум в физических моделях является абстракцией, такой же, как и прозрачная среда. Вернёмся к рассмотрению классической модели электронной дисперсии Лоренца. Относительная диэлектрическая проницаемость среды (77) является комплексной величиной. Выделим в соотношении (77) действительную и мнимую части:

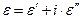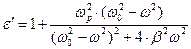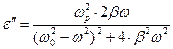, , . (85)

Заметим, что действительная часть комплексной диэлектрической проницаемости является чётной функцией круговой частоты 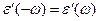, а мнимая часть – нечётной функцией круговой частоты: 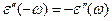. Более того, поскольку 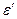и 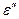зависят от одного и того же набора физических параметров, они не могут рассматриваться как независимые величины. В более полных руководствах показана справедливость аналитических соотношений Крамерса-Кронига, которые обусловлены наличием соответствующей причинно-следственной связи между возмущением электромагнитного поля и реакцией среды.

Дисперсионное уравнение для рассматриваемого случая можно записать в форме:

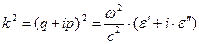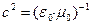, . (86)

Здесь q и p - действительные величины, дисперсионное уравнение записано для случая, когда нормаль к поверхности одинаковой фазы колебаний совпадает с нормалью к поверхности одинаковой амплитуды. Уравнение (86) эквивалентно системе уравнений для действительных величин:

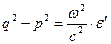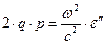, . (87)

Решение системы уравнений (87) с необходимым физическим содержанием имеет вид:

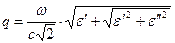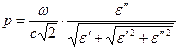, . (88)

Воспользуемся соотношением 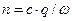и получим для коэффициента преломления:

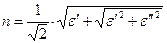. (89)

Если в соотношения (88)-(89) подставить зависимости (85), можно получить явные аналитические выражения для действительной части q и мнимой части p волнового числа k, а также выражение для показателя преломления n. Напомним, что величина p имеет смысл коэффициента поглощения. Графическая иллюстрация полученных результатов приведена на рис. 13.

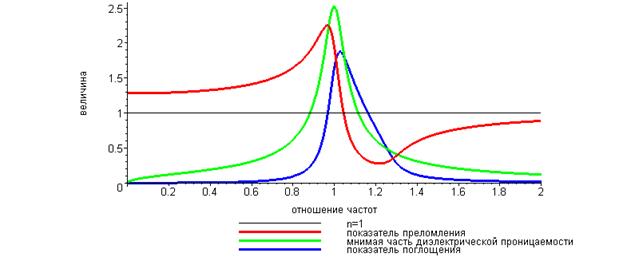
Рис. 13. Дисперсия в среде с поглощением (теория Лоренца).

На рис. 13 по горизонтальной координате отложено отношение круговой частоты электромагнитной волны к собственной круговой частоте колебаний электронов. По вертикали отложены значения показателя преломления n, величина 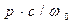, пропорциональная коэффициенту поглощения p, и величина мнимой части 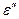комплексной диэлектрической проницаемости 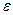. Здесь же для наглядности проведена горизонтальная прямая, соответствующая коэффициенту преломления, равному единице.

Результаты графиков получены при следующих значениях физических параметров: , .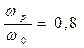

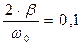Зависимость 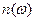на рис. 13 имеет области нормальной дисперсии 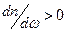и область аномальной дисперсии 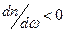. Легко видеть, что коэффициент поглощения имеет заметную величину в области аномальной дисперсии. Заметим, что качественные результаты можно получить, не рассматривая громоздкую формулу для коэффициента поглощения, а анализируя более простую зависимость .

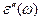Теория Лоренца легко обобщается на случай нескольких собственных частот колебаний электронов, различающихся положением на той или иной электронной оболочке. В реальных условиях, изучая спектры поглощения материальных сред, можно судить о молекулярном строении вещества.