Модулированный по амплитуде «гармонический» сигнал.
Пусть возмущение в начале координат для рассматриваемого случая имеет специфический вид:
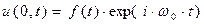 . (34)
. (34)
Параметр 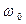 в выражении (34) является несущей частотой гармонических колебаний, переменная во времени амплитуда
в выражении (34) является несущей частотой гармонических колебаний, переменная во времени амплитуда 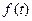 является «огибающей» гармонических колебаний сигнала. Результаты проведённых ниже расчётов получены в предположении, что значение несущей частоты равно
является «огибающей» гармонических колебаний сигнала. Результаты проведённых ниже расчётов получены в предположении, что значение несущей частоты равно 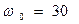 рад-1, значение волнового числа
рад-1, значение волнового числа 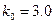 м-1 , огибающая гармонических колебаний «на входе» в волновод имеет вид прямоугольника единичной высоты, она отлична от нуля на интервале времени от -1 до +1 (время измеряется в секундах). Форма огибающей приведена на рис. 5.
м-1 , огибающая гармонических колебаний «на входе» в волновод имеет вид прямоугольника единичной высоты, она отлична от нуля на интервале времени от -1 до +1 (время измеряется в секундах). Форма огибающей приведена на рис. 5.
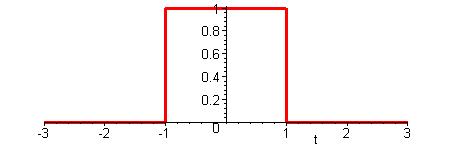
Рис. 5. Огибающая гармонических колебаний на входе в волновод с диспергирующей средой.
Частотный спектр входного сигнала представлен на рис. 6. Здесь следует обратить внимание на то, что максимальная амплитуда гармонических однородных волн соответствует несущей частоте входного сигнала. Подобный результат характерен для «симметричной» формы огибающей.
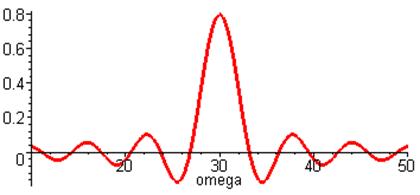
Рис.6. Спектральный состав входного импульса.
Специфическая форма исходного сигнала (34) позволяет получить в аналитической форме и проанализировать некоторые важные результаты, которые характерны для распространения сигналов в диспергирующей среде.
Запишем представление переменой во времени амплитуды 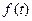 в форме суперпозиции гармонических колебаний:
в форме суперпозиции гармонических колебаний:
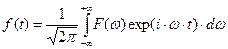 . (35)
. (35)
Это можно сделать с помощью прямого интегрального преобразования Фурье:
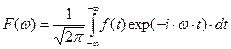 . (36)
. (36)
В этом случае на входе в линейное передающее устройство (волновод, оптическое волокно) имеем совокупность гармонических во времени колебаний:
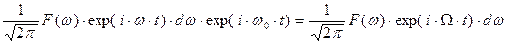 , (37)
, (37)
где по определению
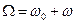 . (38) В силу принципа суперпозиции можно записать зависимость наблюдаемой физической величины от времени в фиксированной точке волновода:
. (38) В силу принципа суперпозиции можно записать зависимость наблюдаемой физической величины от времени в фиксированной точке волновода:
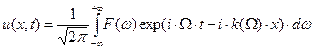 , (39)
, (39)
где функция 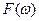 определена соотношение (36). Формально зависимость (39) может быть преобразована к виду:
определена соотношение (36). Формально зависимость (39) может быть преобразована к виду:
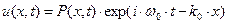 . (40)
. (40)
В выражении (40) явно выделен сомножитель, описывающий гармоническую волну несущей частоты 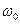 , и выделена зависящая от времени и координаты наблюдения амплитуда сигнала (огибающая колебаний):
, и выделена зависящая от времени и координаты наблюдения амплитуда сигнала (огибающая колебаний):
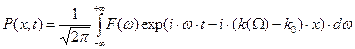 . (41)
. (41)
при вычислении квадратуры (41) приходится учитывать явный вид дисперсионной зависимости
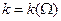 . (42)
. (42)
До сих пор все рассуждения проводились для достаточно общего случая, их общность ограничивалась только условиями существования квадратур, используемых в промежуточных выкладках и окончательных выражениях.
Предположим, что зависимость (42) является аналитической в окрестности значения несущей частоты гармонических колебаний, т.е. справедливо разложение в ряд Тэйлора:
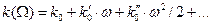 (43)
(43)
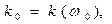
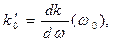
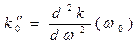 . (44)
. (44)
Таким образом, переменная величина 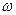 приобретает смысл отклонения от величины несущей частоты колебаний
приобретает смысл отклонения от величины несущей частоты колебаний 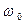 . Часть физически значимых результатов можно получить, рассматривая соответствующее число членов разложения (43). Заметим при этом, что получаемые таким образом результаты имеют приближённый характер и остаются справедливыми только при выполнении соответствующих физических ограничений.
. Часть физически значимых результатов можно получить, рассматривая соответствующее число членов разложения (43). Заметим при этом, что получаемые таким образом результаты имеют приближённый характер и остаются справедливыми только при выполнении соответствующих физических ограничений.
Нулевое приближение. Предположим, что в разложении дисперсионной зависимости (43) выполнены условия:
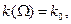
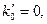
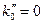 . (45)
. (45)
Остальные члены разложения тождественно равны нулю. Следствием такого предположения является зависимость амплитуды гармонических колебаний несущей частоты от координаты наблюдения и времени:
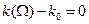
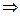
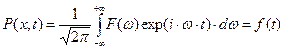 . (46)
. (46)
Полная форма сигнала в точке наблюдения в соответствии с формулой (40) приобретает вид:
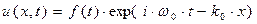 . (47)
. (47)
Проанализируем физическое содержание полученного приближённого решения. Если функция 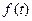 отлична от нуля на интервале от
отлична от нуля на интервале от 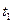 до
до 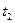 , то в точке наблюдения колебания с несущей частотой начнутся в момент времени
, то в точке наблюдения колебания с несущей частотой начнутся в момент времени 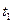 и продолжатся до момента времени
и продолжатся до момента времени 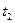 . Физически это означает мгновенное распространение сигнала из начала координат в точку наблюдения, т.е. бесконечную скорость передачи информации. Приходится сделать вывод о том, что рассмотренное приближение является слишком грубым и лишено физического смысла.
. Физически это означает мгновенное распространение сигнала из начала координат в точку наблюдения, т.е. бесконечную скорость передачи информации. Приходится сделать вывод о том, что рассмотренное приближение является слишком грубым и лишено физического смысла.
Первое приближение. Предположим, что в дисперсионной зависимости (43) приняты во внимание нулевой и первый член разложения:
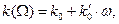
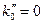 . (48)
. (48)
В показателе экспоненты подынтегральной функции квадратуры (41) множитель перед координатой точки наблюдения принимает вид:
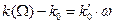 . (49)
. (49)
В этом случае квадратура (41) вычисляется, результатом является соотношение:
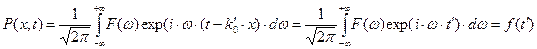 . (50)
. (50)
Теперь можно записать полную форму сигнала в точке наблюдения:
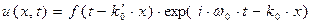 . (51)
. (51)
Перепишем полученное выражение с явным учётом времени запаздывания фазы колебаний несущей частоты и времени запаздывания амплитуды колебаний:
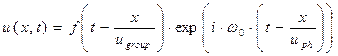 , (52)
, (52)
где использованы определения фазовой и групповой скорости
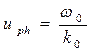 ,
, 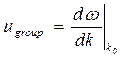 . (53)
. (53)
Соотношение (52) позволяет выявить физическое содержание понятия групповой скорости – это скорость перемещения в пространстве поверхности равной амплитуды.
Именно с этой скоростью происходит распространение сигнала: для его обнаружения необходима отличная от нуля энергия колебаний, которая пропорциональна квадрату модуля амплитуды колебаний. На рис.7 показаны зависимости выходного сигнала от времени для нескольких точек наблюдения, по-разному удалённых от входного сечения волновода.
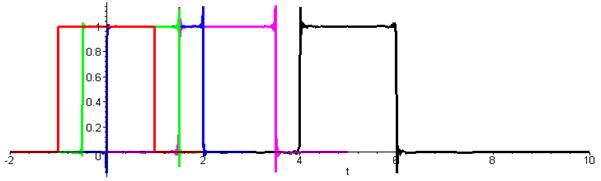
Рис. 7. Зависимости выходного сигнала от времени для точек наблюдения,
удалённых от входного сечения на расстояние 1, 2, 5 и 10 м.
(красная линия – входной сигнал, зелёная – х=1, голубая – х=2,
фиолетовая – х=5, чёрная – х=10, расстояния в метрах)
На рис. 7. имеет смысл обратить внимание на следующие характерные особенности полученного приближения. Во-первых, сохраняется длительность сигнала; во-вторых, сохраняется форма сигнала, последнее позволяет говорить о возможности распознавания сигнала. Правда, этот результат справедлив, если только первое приближение является точным. В общем случае дело усложняется.
Групповая скорость волны может совпадать с фазовой скоростью волны в том случае, если зависимость круговой частоты от волнового числа линейна и однородна: 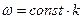 , тогда фазовая скорость волны не зависит от волнового числа, т.е. отсутствует дисперсия.
, тогда фазовая скорость волны не зависит от волнового числа, т.е. отсутствует дисперсия.
Интересно отметить, что различие в распространении одиночной гармонической волны и суперпозиции двух гармонических волн одинаковой амплитуды и бесконечно мало различающихся частот было замечено около 150 лет тому назад. Рассмотрим это явление более подробно. Пусть первая гармоническая волна имеет вид:
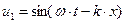 . (54)
. (54)
Вторая гармоническая волна мало отличается от первой:
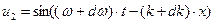 . (55)
. (55)
Результатом сложения описанных волн является волновой процесс значительно более сложной формы:
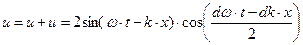 . (56)
. (56)
Перепишем полученное выражение в более наглядной форме:
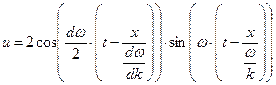 . (57)
. (57)
В этом выражении легко увидеть аналогию с результатом (52):
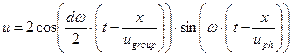 . (58)
. (58)
Физическое содержание зависимости (58) достаточно очевидно: поверхности одинаковых фаз волны большой частоты 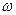 перемещаются в пространстве с фазовой скоростью, а амплитуда этой волны является медленно изменяющейся периодической функцией, зависящей от времени и координаты, причём поверхности одинаковых амплитуд перемещаются в пространстве с групповой скоростью.
перемещаются в пространстве с фазовой скоростью, а амплитуда этой волны является медленно изменяющейся периодической функцией, зависящей от времени и координаты, причём поверхности одинаковых амплитуд перемещаются в пространстве с групповой скоростью.
Элементарный подход к введению понятия групповой скорости (формулы 54-58), конечно, значительно проще, чем рассматриваемый в настоящем разделе, но его неустранимым недостатком является отсутствие возможности установления границ его применимости.
Понятие групповой скорости было введено в научный обиход ирландским математиком и физиком У.Р. Гамильтоном (1805-1865) в 1839 году. Долгое время этот результат приписывали Дж. Стоксу и Дж. Рэлею. Лорд Рэлей (1842-1919) и Дж. У. Гиббс (1839-1903) показали (начало ХХ века), что в опытах Физо и Фуко, проведённых в 1850 г., была измерена именно групповая скорость распространения света в воздухе и в воде, об этом писал и П. Эренфест в 1911 г. Необходимость различать понятия фазовой и групповой скорости была обнаружена при определении показателя преломления среды по явлению преломления светового луча (закон синусов Снеллиуса, определяющая роль фазовой скорости волны) и по скорости распространения сигнала (опыты Физо и Фуко): разница в величинах показателя преломления для одной и той же среды доходила до 0,1. Значение измеряемой величины составляло около 1,5. Такая большая разница значений показателя преломления в оптике считалась катастрофической.
Второе приближение. Теперь допустим, что в дисперсионной зависимости (30) приняты во внимание нулевой, первый и второй члены разложения:
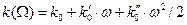 . (59)
. (59)
В показателе экспоненты подынтегральной функции квадратуры (28) множитель перед координатой точки наблюдения принимает вид:
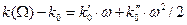 . (60)
. (60)
Если ввести обозначение:
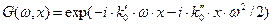 , (61)
, (61)
то зависимость 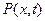 - соотношение (41) – приобретает вид:
- соотношение (41) – приобретает вид:
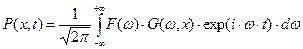 . (62)
. (62)
Если функция 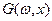 является результатом прямого интегрального преобразования Фурье функции
является результатом прямого интегрального преобразования Фурье функции 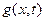 , должна быть справедлива зависимость:
, должна быть справедлива зависимость:
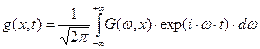 . (63)
. (63)
Интеграл (63) с учетом зависимости (61) является табличным:
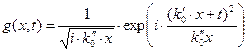 . (64)
. (64)
Поскольку выражение в правой части формулы (62) является обратным интегральным преобразованием Фурье произведения двух прямых интегральных преобразований Фурье, зависимость переменной амплитуды от времени и координаты точки наблюдения является свёрткой двух функций: зависимости от времени амплитуды сигнала в начале координат 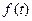 и построенной выше (формула (64)) функции
и построенной выше (формула (64)) функции 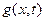 :
:
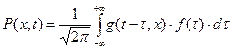 . (65)
. (65)
Результаты расчётов по соотношению (65) приведены на рисунках 8 и 9.
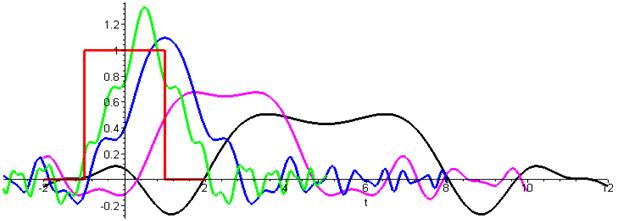
Рис.8. Зависимости выходного сигнала от времени (второе приближение) для точек наблюдения, удалённых от входного сечения на расстояние 1, 2, 5 и 10 м.
(зелёная линия – х=1, голубая – х=2, фиолетовая – х=5, чёрная – х=10, расстояния в метрах)
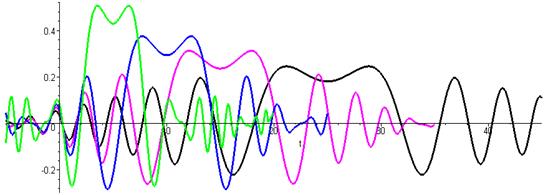
Рис. 9. Зависимости выходного сигнала от времени (второе приближение) для точек наблюдения, удалённых от входного сечения на расстояние 10, 20,30 и 50 м. (зелёная линия – х=10, голубая – х=20, фиолетовая – х=30, чёрная – х=50, расстояния в метрах).
Сравним полученные результаты с результатами первого приближения. Во-первых, легко видеть, что форма выходного сигнала отличается от формы входного сигнала, причём это различие увеличивается с расстоянием до точки наблюдения (сигнал «расплывается»). Во-вторых, в результате второго приближения имеет место возникновение колебаний «на выходе» в моменты времени, когда ещё не было входного сигнала. В-третьих, на больших расстояниях от источника сигнала сигнал становится практически трудно выделяемым на фоне колебаний почти той же амплитуды. Всё это можно объяснить только приближённым характером вычислений.
Кроме того, необходимо отметить, интеграл (50) имеет результатом формулу (64) только при выполнении условия:
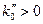
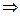
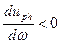
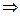
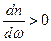 . (66)
. (66)
Условиями (66) определяется явление «нормальной дисперсии»: показатель преломления, определяемый по фазовой скорости волны, должен увеличиваться с возрастанием частоты 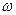 . Явление аномальной дисперсии
. Явление аномальной дисперсии 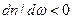 , как правило, связано с явлением поглощения волны в материальной среде. Качественное объяснение закономерностей явления дисперсии электромагнитных волн может быть построено на основе электронной теории дисперсии Х.А. Лоренца (1853-1928).
, как правило, связано с явлением поглощения волны в материальной среде. Качественное объяснение закономерностей явления дисперсии электромагнитных волн может быть построено на основе электронной теории дисперсии Х.А. Лоренца (1853-1928).
Дата добавления: 2017-09-01; просмотров: 1394;











