Плоские гармонические электромагнитные волны в однородной проводящей анизотропной среде.
Рассмотрим систему уравнений электродинамики для случая однородной анизотропной проводящей среды:
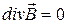 (1)
(1)
 (2)
(2)
 (3)
(3)
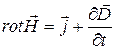 (4)
(4)
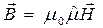 ,
, 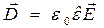 ,
, 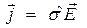 , (5)
, (5)
где треугольная крышка над символом физической величины означает тензор второго ранга. Развёрнутая форма записи материальных уравнений (5)
 (51)
(51)
 (52)
(52)
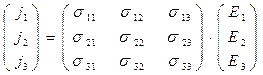 (53)
(53)
Заметим, что коэффициенты пропорциональности в материальных уравнениях (5) анизотропной среды могут являться функциями частоты w. Физический смысл соотношений (5) состоит в том, что в случае анизотропных сред векторы  и
и 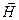 , также как и векторы
, также как и векторы 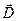 и
и 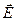 или векторы
или векторы 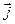 и
и 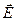 не являются параллельными друг другу: величина фиксированной проекции первого вектора зависит от всех проекций второго вектора. В случае «слабых» полей и выполнения некоторых дополнительных условий на свойства среды эта зависимость является однородной и линейной. Термодинамический и молекулярно-кинетический анализ свойств реальных сред позволяет установить определенные свойства симметрии тензоров
не являются параллельными друг другу: величина фиксированной проекции первого вектора зависит от всех проекций второго вектора. В случае «слабых» полей и выполнения некоторых дополнительных условий на свойства среды эта зависимость является однородной и линейной. Термодинамический и молекулярно-кинетический анализ свойств реальных сред позволяет установить определенные свойства симметрии тензоров 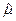 ,
, 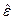 и
и  , положительность их составляющих и т.п. В настоящем разделе предполагается использовать тензорные операции в декартовой системе координат. Заметим, что описание анизотропных сред кристаллической структуры с неортогональными осями симметрии требует применения тензорного аппарата в косоугольных координатах, что сопряжено с дополнительными математическими усложнениями.
, положительность их составляющих и т.п. В настоящем разделе предполагается использовать тензорные операции в декартовой системе координат. Заметим, что описание анизотропных сред кристаллической структуры с неортогональными осями симметрии требует применения тензорного аппарата в косоугольных координатах, что сопряжено с дополнительными математическими усложнениями.
При изучении плоских электромагнитных волн в анизотропной среде будем предполагать, что физические величины 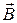 ,
, 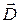 ,
, 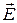 ,
, 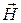 ,
, 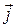 и r описываются выражениями вида
и r описываются выражениями вида
 (6)
(6)
где 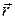 – радиус-вектор точки наблюдения, t – время,
– радиус-вектор точки наблюдения, t – время, 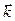 – комплексный (в общем случае) волновой вектор, w – частота волны. Комплексный вектор
– комплексный (в общем случае) волновой вектор, w – частота волны. Комплексный вектор 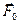 является постоянной векторной величиной, которая не зависит от координат и времени. В этом случае справедливы соотношения:
является постоянной векторной величиной, которая не зависит от координат и времени. В этом случае справедливы соотношения:
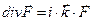 ,
, 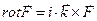 ,
, 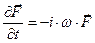 . (7)
. (7)
Для комплексных амплитуд, упомянутых выше физических величин, из системы (1)-(4) с учетом выражения (7) получаем систему уравнений:
 , (8)
, (8)
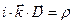 , (9)
, (9)
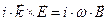 , (10)
, (10)
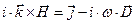 . (11)
. (11)
При записи системы уравнений (8)-(11) специального обозначения для комплексной амплитуды физической величины не вводилось. Соотношения (5) справедливы и для системы (8)-(11) с учетом физического смысла символа.
Плоская гармоническая электромагнитная волна является специфическим физическим процессом. Для этого процесса, как легко видеть, уравнение (8) является следствием уравнения (10)

и поэтому может быть исключено из рассмотрения. Что же касается уравнения (9), то вопрос о его значимости в системе основных уравнений плоских гармонических электромагнитных волн требует обсуждения. Умножим уравнение (11) скалярно на вектор 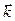 :
:
 .
.
Правую часть полученного соотношения можно умножить на мнимую единицу:
 . (12)
. (12)
В результате получено уравнение сохранения электрического заряда в дифференциальной форме. Это не удивительно, поскольку закон сохранения электрического заряда можно рассматривать как следствие системы уравнений Максвелла.
Из цепочки соотношений (12) нельзя сделать заключение, что правая часть уравнения (9) обращается в ноль в произвольном случае. Но обычно и уравнение (9) специально не рассматривают, полагая, что оно выполняет роль определения для величины 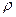 .
.
Перепишем уравнения (10) и (11) с использованием материальных уравнений среды:
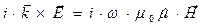 , (13)
, (13)
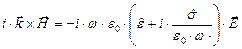 . (14)
. (14)
Введём в рассмотрение комплексный тензор диэлектрической проницаемости среды:
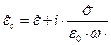 (15)
(15)
Это оказывается удобным, поскольку уравнение (14) принимает вид
 , (16)
, (16)
совпадающий по форме с уравнением полного тока для среды без поглощения. Из уравнения (16) следует уравнение
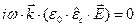 , (17)
, (17)
но это не означает выполнения условия
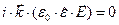 . (18)
. (18)
Таким образом, в общем случае волна объёмной плотности свободных электрических зарядов может существовать. Эта волна исчезает, если тензор электропроводности 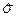 пропорционален тензору диэлектрической проницаемости
пропорционален тензору диэлектрической проницаемости  :
:
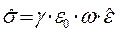
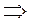
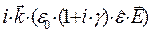
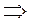
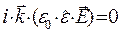
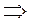
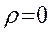 . (19)
. (19)
В специальной литературе встречается утверждение, что для выполнения условия  достаточно того, чтобы главные оси тензора диэлектрической проницаемости и тензора электропроводности совпадали. Напомним, что для тензора второго ранга можно подобрать такую систему координат, чтобы матрица тензора стала диагональной. Приведённое утверждение подразумевает, что эта специфическая система координат должна быть одна и та же для обоих тензоров. Но этого недостаточно, необходимо ещё выполнение условия пропорциональности:
достаточно того, чтобы главные оси тензора диэлектрической проницаемости и тензора электропроводности совпадали. Напомним, что для тензора второго ранга можно подобрать такую систему координат, чтобы матрица тензора стала диагональной. Приведённое утверждение подразумевает, что эта специфическая система координат должна быть одна и та же для обоих тензоров. Но этого недостаточно, необходимо ещё выполнение условия пропорциональности:
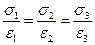 . (20)
. (20)
Индексами 1,2,3 в соотношениях (20) отмечены диагональные элементы соответствующих тензоров после приведения к диагональному виду. Условия (19) в этом смысле более удобны, можно говорить, что они являются первичными условиями обращения волны объёмной плотности свободных электрических зарядов в ноль.
Вернёмся к рассмотрению уравнения (16). Если матрица тензора 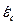 не является особенной, т.е. её детерминант не равен нулю, то существует матрица
не является особенной, т.е. её детерминант не равен нулю, то существует матрица 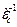 , обратная по отношению к матрице тензора
, обратная по отношению к матрице тензора 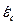 :
:
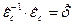 , (21)
, (21)
где 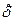 - «единичная матрица», её недиагональные члены равны нулю, а диагональные равны единице, её основное свойство состоит в том, что она в результате умножения на вектор не меняет компоненты этого вектора:
- «единичная матрица», её недиагональные члены равны нулю, а диагональные равны единице, её основное свойство состоит в том, что она в результате умножения на вектор не меняет компоненты этого вектора:
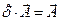 . (22)
. (22)
Умножая слева обе части уравнения (16) на матрицу 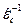 , получаем:
, получаем:
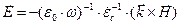 . (23)
. (23)
Явное выражение вектора напряжённости электрического поля (23) подставим в уравнение электромагнитной индукции (13):
 . (24)
. (24)
Уравнение (24) является линейным векторно-матричным однородным уравнением относительно вектора  . Его нетривиальное решение возможно только при выполнении специальных условий, налагаемых на компоненты волнового вектора
. Его нетривиальное решение возможно только при выполнении специальных условий, налагаемых на компоненты волнового вектора 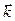 . Получить явную аналитическую форму этих условий наиболее просто можно при помощи математического приёма формальной замены векторного произведения (символическая форма записи) на векторно-матричную форму записи той же операции. Введём в рассмотрение тензор
. Получить явную аналитическую форму этих условий наиболее просто можно при помощи математического приёма формальной замены векторного произведения (символическая форма записи) на векторно-матричную форму записи той же операции. Введём в рассмотрение тензор 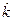
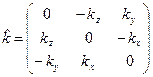 . (25)
. (25)
Тензор 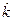 называют «дуальным» по отношению к исходному вектору
называют «дуальным» по отношению к исходному вектору 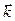 , с использованием которого он построен. Замечательное свойство тензора
, с использованием которого он построен. Замечательное свойство тензора 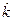 состоит в том, что компоненты произведения
состоит в том, что компоненты произведения 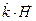 совпадают с проекциями на оси декартовой системы координат векторного произведения
совпадают с проекциями на оси декартовой системы координат векторного произведения  , что легко проверяется непосредственным вычислением. Воспользуемся этим свойством для преобразования уравнения (24):
, что легко проверяется непосредственным вычислением. Воспользуемся этим свойством для преобразования уравнения (24):
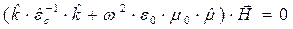 . (26)
. (26)
Левая часть уравнения (26) представляет собой произведение матрицы на вектор-столбец, а уравнение в целом – векторно-матричное линейное однородное уравнение относительно компонент вектора  . Теперь условие существования нетривиального решения приобретает хорошо знакомый вид:
. Теперь условие существования нетривиального решения приобретает хорошо знакомый вид:
 . (27)
. (27)
Поскольку матрица тензора 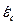 имеет комплексные компоненты, очевидно, что её обратная матрица
имеет комплексные компоненты, очевидно, что её обратная матрица 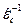 тоже является комплексной. В этом случае и матрица
тоже является комплексной. В этом случае и матрица 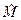 и её детерминант являются комплексными. Таким образом, уравнение (27) фактически является системой двух вещественных уравнений:
и её детерминант являются комплексными. Таким образом, уравнение (27) фактически является системой двух вещественных уравнений:
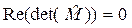 ,
, 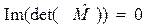 . (28)
. (28)
Предвосхищая последующие результаты, воспользуемся общей формой записи волнового вектора
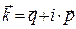 , (29)
, (29)
которая была использована в предыдущих разделах. Удобно при записи декартовых составляющих вещественных векторов 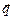 и
и  перейти к сферическим координатам
перейти к сферическим координатам
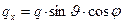 ,
, 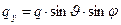 ,
, 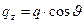 ,
,
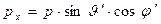 ,
, 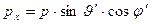 ,
, 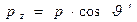 .
.
Если эти выражения использовать в уравнениях (28), то можно получить систему двух уравнений относительно величин q и p:
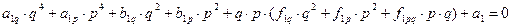 , (30)
, (30)
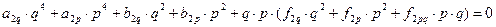 . (31)
. (31)
Коэффициенты этих уравнений являются функциями угловых переменных (ориентация в пространстве векторов 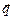 и
и  ), физических свойств среды (компоненты тензоров диэлектрической проницаемости, магнитной проницаемости и электропроводности среды) и частоты электромагнитной волны
), физических свойств среды (компоненты тензоров диэлектрической проницаемости, магнитной проницаемости и электропроводности среды) и частоты электромагнитной волны 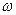 . Заметим, что величины q и p должны быть вещественными и положительно определёнными величинами, только при выполнении этих ограничений решение будет обладать физическим смыслом.
. Заметим, что величины q и p должны быть вещественными и положительно определёнными величинами, только при выполнении этих ограничений решение будет обладать физическим смыслом.
Располагая совокупностью решений системы уравнений (30)-(31)
 ,
,  ,
,  , (32)
, (32)
где А11, А12 и А13 являются детерминантами второго порядка, получающегося из матрицы 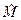 вычёркиванием соответствующей строки и соответствующего столбца, а величина
вычёркиванием соответствующей строки и соответствующего столбца, а величина 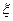 является параметром решения, можно изучать конкретные формы плоских неоднородных электромагнитных волн:
является параметром решения, можно изучать конкретные формы плоских неоднородных электромагнитных волн:
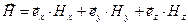 , (33)
, (33)
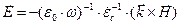 . (34)
. (34)
Заметим, что однопараметрическое представление решения (32) действительно является решением системы уравнений (30)-(31), если не все величины А11, А12 и А13 обращаются в нуль.
Подводя итоги рассмотрения распространения плоских электромагнитных волн в однородной не изотропной проводящей среде, заметим, что нам удалось познакомиться с методом исследования и получить общие результаты, детальное исследование выходит за рамки настоящего пособия. Подробно эти явления и наблюдаемые при этом эффекты рассматриваются в специальных руководствах по оптике, кристаллооптике и металлооптике.
Формулы Френеля.
Френель считал, что само существование световых волн обусловлено динамическими свойствами светоносного эфира. В те годы концепция «эфира» была распространённой научной гипотезой. Френель считал, что колебания, из которых состоит свет, перпендикулярны направлению распространения волны (гипотеза о поперечном характере световых волн). Он согласен с Т. Юнгом в том, что явления отражения и преломления вызваны разностью инерционных свойств светоносного эфира, заполняющего различные материальные среды. Одно из основных предположений Френеля состоит в том, что «инерция эфира» обратно пропорциональна квадрату скорости света в среде. На поверхности раздела двух сред геометрические смещения соседних молекул должны быть параллельны плоскости раздела и одинаковы в обеих средах (условие непрерывности касательных компонент смещения). Кроме того, на границе раздела сред должен выполняться закон сохранения энергии. Это условие формулируется так: поток энергии падающей волны через элемент поверхности раздела сред равен сумме потоков энергии отражённой и преломлённой волн через этот же элемент поверхности раздела сред. Заметим, что представления Френеля во многом являются механистическими. Ниже мы ещё вернёмся к анализу этих представлений, а пока рассмотрим его результаты.
 Произвольные поперечные колебания эфира в световой волне можно разложить на колебания, перпендикулярные плоскости падения, и параллельные плоскости падения волны. Плоскость падения волны образована вектором направления распространения волны и вектором нормали к поверхности раздела сред. На рис. ???? плоскость падения является плоскостью рисунка. Удобно рассматривать по отдельности волны с первой и второй ориентацией направления колебаний, а результаты потом «сложить».
Произвольные поперечные колебания эфира в световой волне можно разложить на колебания, перпендикулярные плоскости падения, и параллельные плоскости падения волны. Плоскость падения волны образована вектором направления распространения волны и вектором нормали к поверхности раздела сред. На рис. ???? плоскость падения является плоскостью рисунка. Удобно рассматривать по отдельности волны с первой и второй ориентацией направления колебаний, а результаты потом «сложить».
Рассмотрим первый случай (рис. ). Пусть 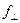 ,
, 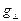 и
и 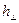 представляют собой амплитуды падающей, отражённой и преломлённой волн, угол падения
представляют собой амплитуды падающей, отражённой и преломлённой волн, угол падения 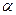 равняется углу отражения, угол преломления обозначим величиной
равняется углу отражения, угол преломления обозначим величиной 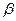 . Световая волна падает из первой среды и преломляется во второй среде. Крестиками в кружках условно обозначены направления колебаний. В соответствии с представлениями Френеля плотность потоков энергии в каждой из волн пропорциональна выражениям:
. Световая волна падает из первой среды и преломляется во второй среде. Крестиками в кружках условно обозначены направления колебаний. В соответствии с представлениями Френеля плотность потоков энергии в каждой из волн пропорциональна выражениям:
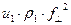 ,
,  ,
, 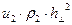 . (1)
. (1)
Здесь 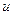 - скорость волны,
- скорость волны, 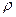 - «инерция эфира». Плотность потока энергии в световой волне направлена вдоль соответствующего направления распространения волны. Запишем условие энергетического баланса для единичного элемента поверхности раздела сред и условие непрерывности касательных компонент смещения:
- «инерция эфира». Плотность потока энергии в световой волне направлена вдоль соответствующего направления распространения волны. Запишем условие энергетического баланса для единичного элемента поверхности раздела сред и условие непрерывности касательных компонент смещения:
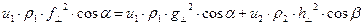 , (2)
, (2)
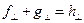 . (3)
. (3)
Дополним рассматриваемую математическую модель явления законом Снеллиуса
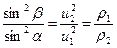 . (4)
. (4)
Из системы уравнений (2)-(4) получаются следующие зависимости:
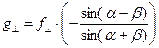 ,
,  . (5)
. (5)
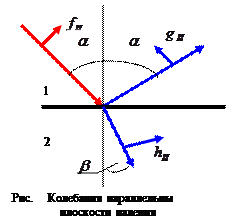 В соответствии с полученными результатами колебания в преломлённой волне всегда совпадают по фазе с колебаниями в падающей волне, а фаза колебаний в отражённой волне испытывает скачок на величину полупериода, если вторая среда является оптически более плотной, и не испытывает скачка, если вторая среда является оптически менее плотной.
В соответствии с полученными результатами колебания в преломлённой волне всегда совпадают по фазе с колебаниями в падающей волне, а фаза колебаний в отражённой волне испытывает скачок на величину полупериода, если вторая среда является оптически более плотной, и не испытывает скачка, если вторая среда является оптически менее плотной.
Рассмотрим второй случай: колебания в падающей, отражённой и преломлённой волнах происходят в направлении, параллельном плоскости падения волны (рис. ).
Плотности потоков энергии для рассматриваемых волн теперь описываются выражениями:
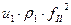 ,
, 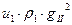 ,
, 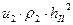 . (6)
. (6)
Баланс потоков энергии при переходе через границу раздела приобретает вид:
 . (7)
. (7)
Условие непрерывности касательных составляющих смещения записывается в форме:
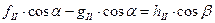 . (8)
. (8)
В дополнение к уравнениям (7) и (8) остаётся справедливым и уравнение (4).
Решение системы уравнений (7)-(8) и (4) приводит к соотношению:
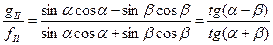 . (9)
. (9)
Соотношение (9) известно в оптике как закон тангенсов Френеля. Для амплитуды преломлённой волны получается соотношение:
 . (10)
. (10)
В случае нормального падения световой волны на плоскую границу раздела двух сред формулы Френеля значительно упрощаются. С помощью предельного перехода 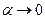
(при этом, естественно, и  получаем для абсолютных величин амплитуд колебаний в падающей, отражённой и преломлённой волн произвольной поляризации:
получаем для абсолютных величин амплитуд колебаний в падающей, отражённой и преломлённой волн произвольной поляризации:
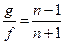 ,
, 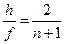 . (11)
. (11)
Здесь 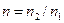 - относительный показатель преломления. Наличие отражённой световой волны можно рассматривать как «потери» светового потока при прохождении границы раздела двух сред. Примечательно, что при переходе световой волны из воздуха в стекло (
- относительный показатель преломления. Наличие отражённой световой волны можно рассматривать как «потери» светового потока при прохождении границы раздела двух сред. Примечательно, что при переходе световой волны из воздуха в стекло ( 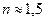 ) амплитуда отражённой волны составляет 0,2 от амплитуды падающей волны, а интенсивность, которая пропорциональна квадрату амплитуды, – всего 4% от интенсивности падающей волны. Практический вывод из этого результата: просветляющая плёнка на поверхности очков мало эффективна и практически бесполезна, заметный положительный эффект достигается только в сложных оптических многолинзовых системах при исследовании слабо светящихся объектов.
) амплитуда отражённой волны составляет 0,2 от амплитуды падающей волны, а интенсивность, которая пропорциональна квадрату амплитуды, – всего 4% от интенсивности падающей волны. Практический вывод из этого результата: просветляющая плёнка на поверхности очков мало эффективна и практически бесполезна, заметный положительный эффект достигается только в сложных оптических многолинзовых системах при исследовании слабо светящихся объектов.
Из теории Френеля следует интересное явление, открытое экспериментально ещё в 1815 г. Дэвидом Брюстером (1781-1868). Оказывается, что при выполнении условия 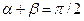 (угол падения при этом называют углом Брюстера) амплитуда отражённой волны
(угол падения при этом называют углом Брюстера) амплитуда отражённой волны 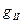 обращается в нуль. Если в исходной падающей волне имели место колебания, параллельные плоскости падения и перпендикулярные ей, то в отражённой волне остались только колебания, направление которых перпендикулярно плоскости падения: из произвольной световой волны получилась плоско поляризованная световая волна.
обращается в нуль. Если в исходной падающей волне имели место колебания, параллельные плоскости падения и перпендикулярные ей, то в отражённой волне остались только колебания, направление которых перпендикулярно плоскости падения: из произвольной световой волны получилась плоско поляризованная световая волна.
Интересно, что Брюстер (член Лондонского Королевского общества и президент Эдинбургского Королевского общества) в своё время был больше известен как изобретатель калейдоскопа, чем своими работами в области кристаллооптики.
Дата добавления: 2017-09-01; просмотров: 1645;











