Электромагнитные волны.

Система уравнений Максвелла допускает существование переменного электромагнитного поля в вакууме в форме электромагнитных волн. Однородные уравнения системы уравнений Максвелла для рассматриваемого случая имеют вид:

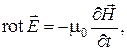(1)

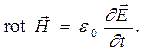(2)

Вычислим, например, ротор от обеих частей уравнения (1):

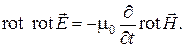(3)

Из векторного анализа известно, что

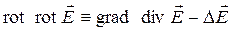, (4)

оператор Лапласа 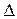в выражении (4) применяется к каждой компоненте векторного поля .

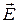Из уравнения (1.3) исходной системы уравнений Максвелла для рассматриваемого случая имеем

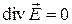, (5)

что с учетом уравнения (4) позволяет получить

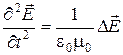. (6)

В одномерном случае из уравнения (6) следует

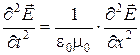(7)

(для каждой компоненты вектора ).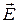

Сравнивая уравнение (7) с уравнением

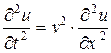, (8)

описывающим распространение бегущей волны с фазовой скоростью 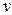вдоль оси 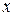, находим, что

а) каждая из компонент вектора 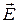описывается волновым уравнением, т. е. представляет собой волну, бегущую вдоль оси ;

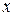б) фазовая скорость этой волны равна

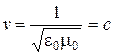, (9)

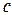- скорость света (здесь использованы теоретические значения электрической и магнитной постоянных).

Заметим, что можно было бы провести выкладки, вычисляя ротор от обеих частей уравнения (2) и исключая поле 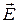из получающегося уравнения с помощью уравнения (1). На этом пути приходят к уравнению

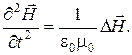(10)

Оказывается, что и векторное поле 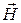имеет волновой характер, причем фазовая скорость волны 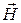совпадает с фазовой скоростью волны .

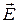Анализ системы уравнений (6) и (10) на первый взгляд приводит к выводу, что волны 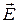и 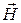совершенно независимы друг от друга. На самом деле это не так. Если исследовать решения уравнений (1) и (2) непосредственно, оказывается, что плоские волны 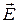и 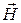являются поперечными волнами, они специальным образом ориентированы друг относительно друга, имеют одну и ту же начальную фазу колебаний и согласованные между собой амплитуды. Частоты и волновые векторы у этих волн одинаковы. Всё это справедливо для однородной изотропной среды, не проводящей электрический ток, и неограниченного пространства. Для электромагнитных волн, распространяющихся в проводящей среде (среда с поглощением электромагнитной энергии) и (или) в волноводах с конечными размерами поперечного сечения, результаты будут более сложными. С основными закономерностями распространения электромагнитных волн можно познакомиться в руководствах по теории электромагнитных волн или в оптике.

Интересно, почему система уравнений (6), (10) не позволяет все это обнаружить? Дело в том, что система (6), (10) получена из исходных уравнений (1)-(2) дифференцированием: исходная система - это система двух дифференциальных уравнений первого порядка, а конечная - система двух уравнений второго порядка. Повышение порядка производных в уравнении расширяет класс допустимых решений. Формально независимые волны 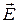и 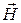как решения системы (6), (10) содержат, в частности, и такие, которые являются решениями системы (1)-(2) с описанными выше свойствами, т. е. реальные электромагнитные волны.

В реальной бегущей электромагнитной волне отличен от нуля средний по времени вектор Умова-Пойнтинга

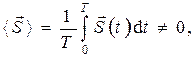(11)

что позволяет говорить о том, что бегущая электромагнитная волна переносит энергию. Среднее по времени значение 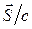является средней по времени плотностью потока импульса, а величина 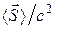- средняя по времени плотность потока “массы”, переносимой электромагнитной волной (полезно сравнить эти соотношения с определением вектора 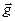предыдущего раздела).

Наличие ненулевой величины плотности импульса теоретически позволяет рассчитать силу давления, которое оказывает электромагнитная волна на твердую не абсолютно прозрачную поверхность. В момент создания системы уравнений Максвелла экспериментально электромагнитные волны не были известны. Их несколько позже, в 1888 г., обнаружил Г.Герц (1857-1894). Интересно, что первая в истории человечества радиограмма (Александр Попов) состояла всего из двух слов: «Генрих Герц».

Тот факт, что свет является совокупностью электромагнитных волн, стало неоспоримым после знаменитых опытов П.Н. Лебедева (1866-1912) по измерению давления света на твёрдую поверхность (1899 г.) и на газы (1907 г.). Интересно, что о давлении света писали такие выдающиеся физики как И. Кеплер (1619 г.) и Л. Эйлер (1748 г.). Исходя из термодинамических законов А. Бартоли (1876 г.) и Л. Больцман (1884 г.) теоретически определили давление излучения.

Знаменитый английский физик У. Томсон (1824-1907) – лорд Кельвин - говорил, что он всю жизнь воевал с Максвеллом, не признавая светового давления, а П.Н. Лебедев заставил его сдаться перед его опытами.

Теория электродинамики Максвелла стала общепризнанной.