Распространение произвольного сигнала в линейной диспергирующей среде.

Допустим, что для одиночной гармонической волны справедлива одна из зависимостей (дисперсионное уравнение позволяет переходить от одной зависимости к другой):

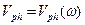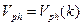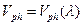, , . (22)

Зависимости (22) не обязательно являются следствием конкретного уравнения (18), здесь и ниже закон дисперсии рассматривается для достаточно общего случая.

Произвольный сигнал, как известно, представляет собой суперпозицию гармонических волн. Пусть в начале координат имеет место произвольная зависимость рассматриваемой физической величины от времени.

Рассмотрим точное решение. Если зависимость физической величины от времени в начале координат имеет вид

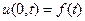, (23)

при выполнении определённых условий её можно представить в форме суперпозиции гармонических колебаний:

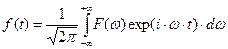. (24)

Формально соотношение (11) является обратным интегральным преобразованием Фурье. В курсе математического анализа доказывается, что обратное интегральное преобразование Фурье связано с прямым интегральным преобразованием Фурье:

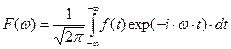(25)

Для наших целей достаточно знать, что по произвольной (но «хорошей») функции 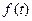можно вычислить её «изображение» по Фурье (25), с помощью которого получить представление функции 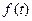в форме суперпозиции гармонических колебаний (24). Для бесконечно малого интервала круговой частоты 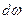можно рассмотреть гармоническое колебание с круговой частотой 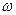и амплитудой

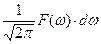. (26)

Такое гармоническое колебание в начале координат генерирует гармоническую волну вида:

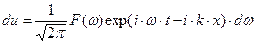. (27)

В силу принципа суперпозиции искомое решение можно записать в форме квадратуры:

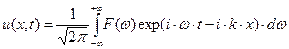, (28)

при вычислении интеграла (28) необходимо учитывать конкретный закон дисперсии

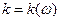. (29)

Формальное решение (28) не очень удобно для анализа. Введём обозначение

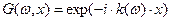(30)

и перепишем выражение 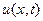в форме «свёртки»:

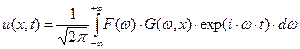. (31)

Если существует обратное интегральное преобразование Фурье для функции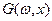

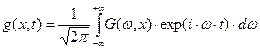, (32)

то имеет место результат:

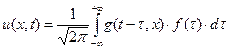. (33)

Результат (33) становится очевидным, если рассмотреть цепочку соотношений, обоснованность которых покоится на введённых определениях и возможности изменения порядка интегрирования по бесконечному промежутку: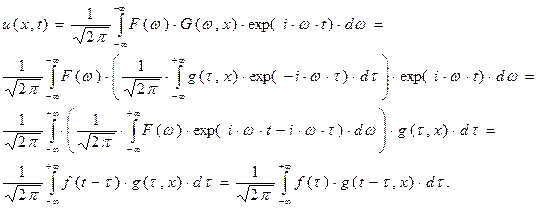

В курсах математического анализа подробно обсуждаются условия, когда подобные выкладки действительно справедливы.

Трудности практического использования решения в форме зависимости (33) заключаются в вычислении квадратуры (32) с учётом определения (30). Зависимость (33) предпочтительнее зависимости (28) в смысле наглядности: зависимость от времени возмущения в начале координат явно входит подынтегральное выражение. Но в выражении (28) есть свои преимущества: в нём явно подчёркивается волновой характер процесса.

Заметим, что характерные стороны распространения заданного в начале координат сигнала как функции времени можно обнаружить, используя для моделирования процесса современные системы вычислительной математики, например, универсальную систему Matlab, или специализированные пакеты моделирования волновых процессов.