Сложение ускорений в сложном движении точки

Абсолютное ускорение точки определим вычислением полной производной по времени от абсолютной скорости (2.38)

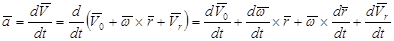(2.40)

Для полных производных по времени векторов применим формулу Бура. Получим

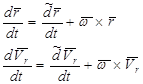(2.41)

Подставляя выражения (2.41) в зависимость (2.40) получим

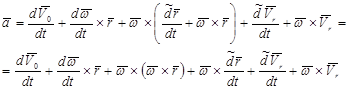
Учитывая, что

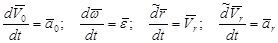
выражение для полного ускорения примет вид

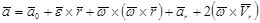(2.42)

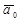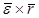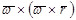В этой формуле первые три слагаемых составляют ускорение точки свободного твердого тела в общем случае его движения вместе с подвижной системой осей координат относительно неподвижной системы осей координат. Первое слагаемое - ускорение точки О, и - соответственно вращательное и осестремительное ускорение точки М, если бы она двигалась только вместе с подвижной системой осей координат, не имея в рассматриваемой момент времени относительного движения. С учетом этого выражение (2.42) примет вид

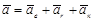(2.43)

где 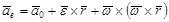(2.44)

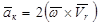(2.45)

По определению 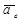является переносным ускорение точки, ускорение 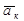называют ускорением Кориолиса.

Зависимость (2.43) выражает теорему сложения ускорений точки: абсолютное ускорение точки является векторной суммой трех ускорений – переносного, относительного и Кориолиса.

Для определения переносного ускорения используется кинематика движения свободного твердого тела. В частном случае, когда переносное движение является вращением твердого тела вокруг неподвижной оси, переносное ускорение равно .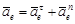

Для определения относительного ускорения используется кинематика точки. При естественном способе задания движения

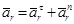
Абсолютное ускорение в этом случае

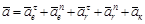
2.5.3. Ускорение Кориолиса.

Рассмотрим ускорение Кориолиса и его свойства. Оно определяется формулой (2.45)

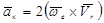
Угловую скорость подвижной системы отсчета, то есть угловую скорость переносного движения , заменили на .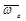

Ускорение Кориолиса является результатом взаимного влияния двух движений – переносного и относительного. Часть его 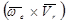получается в следствии изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже равная 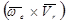, есть результат изменения относительной скорости в следствии переносного движения. Это следует из анализа формул при выводе абсолютного ускорения.

Модуль ускорения Кориолиса в соответствии с (2.45) определяется выражением

(2.46)

Для определения ускорения Кориолиса удобно применять правило Жуковского. Пусть имеем т.М, движущуюся с относительной скоростью 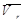(рис. 2.2.9).

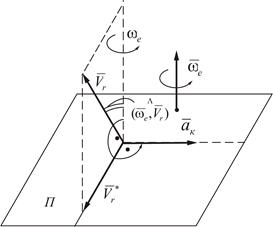
Рисунок 2.29. К определению направления ускорения Кориолиса

Построим плоскость П, перпендикулярную угловой скорости переносного вращения 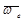и спроектируем 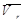на эту плоскость. Проекцию обозначим . .

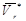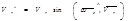Ускорение Кориолиса выразится в форме

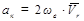(2.47)

Правило Жуковского: модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направления ускорения Кориолиса следует вектор проекции относительной скорости 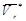повернуть на 90⁰ вокруг оси, параллельной оси переносного вращения в направлении этого вращения.