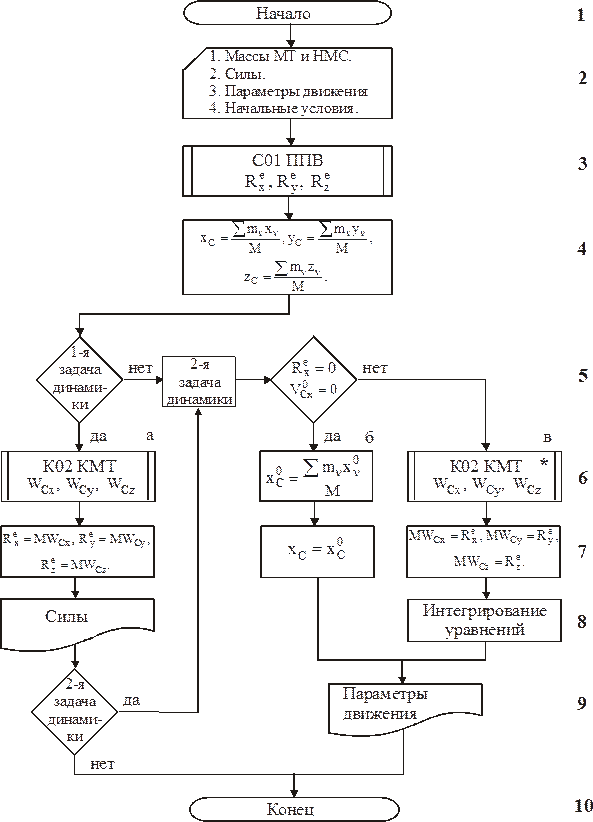
Алгоритм решения задач с помощью теоремы о движении центра масс СМТ – схема алгоритма
Д45 ЦМС с комментариями и примерами
Комментарии
К.2.Рассматриваемый объект принимается за МС, указывается система отсчета, в которой исследуется ее движение. Выделяются и нумеруются МТ и НМС, входящие в МС. На чертеже изображается силовая схема, т.е. рисуются все внешние силы и моменты, действующие на МС, в том числе внешние пассивные силы и моменты – реакции связи на основании принципа освобождаемости от связей (аксиома 5 статики). Формулируются начальные условия.
К.3, 4. Находятся проекции главного вектора внешних сил и радиуса-вектора центра масс только на те направления (оси), вдоль которых необходимо определить силы (1-я задача динамики) и перемещения или кинематические параметры (2-я задача динамики).
Координаты центра масс МС вычисляются для текущего или заданного момента времени через заданные размеры и параметры движения. Для определения координат центра масс может быть использована схема алгоритма С08 ОЦТ (Ч.2 Статика), а в случае сложного движения МТ, входящей в МС, алгоритм К07 СДТ (Ч.1 Кинематика).
К.5.б.Для случая 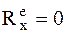 и
и 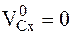 ось x выбрана для определенности. В реальной задаче такой осью может быть любая другая.
ось x выбрана для определенности. В реальной задаче такой осью может быть любая другая.
К.8.в.При интегрировании используются либо метод разделения переменных, либо теория линейных дифференциальных уравнений первого и второго порядков. Постоянные интегрирования находятся с помощью начальных условий.
Примечание
Теорема о движении центра масс МС чаще всего применяется в случаях, когда НМС совершает поступательное движение, а МТ - любое движение, для определения перемещений того или иного объекта и для определения пассивных сил – реакций связи, вызванных этими перемещениями.
Пример 1
2 Электрический мотор массы 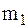 установлен без крепления на негладком горизонтальном фундаменте (коэффициент трения скольжения f). На валу мотора под прямым углом закреплен одним концом однородный стержень длиной 2l и массы
установлен без крепления на негладком горизонтальном фундаменте (коэффициент трения скольжения f). На валу мотора под прямым углом закреплен одним концом однородный стержень длиной 2l и массы 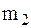 . На другой конец стержня насажен точечный груз массы
. На другой конец стержня насажен точечный груз массы 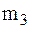 (рис. 31). Угловая скорость вала постоянна и равна
(рис. 31). Угловая скорость вала постоянна и равна 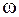 . Определить суммарную силу давления
. Определить суммарную силу давления 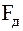 на фундамент, горизонтальное перемещение мотора и условия, при которых мотор будет подпрыгивать, не будучи прикреплен болтами.
на фундамент, горизонтальное перемещение мотора и условия, при которых мотор будет подпрыгивать, не будучи прикреплен болтами.
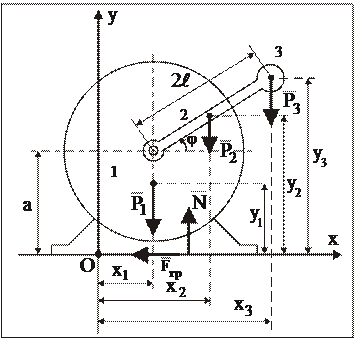
Рис. 31
В начальный момент мотор находится в покое и стержень горизонтален. Ось х горизонтальна, ось у проходит через вал в начальный момент времени.
МС состоит из: двух АТТ (мотор и стержень) и МТ (груз).
 3С04 ППВ
3С04 ППВ
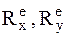
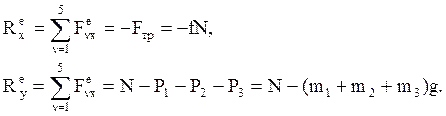
Обозначим координаты центра масс мотора через х1, у1, центра масс стержня х2, у2, и координаты груза х3, у3 в момент времени t. Координаты центра масс стержня и груза записы-ваются с учетом того, что они участвуют в сложном движении (переносном движении вместе с мотором и относительном вращательном движении относительно мотора).
4 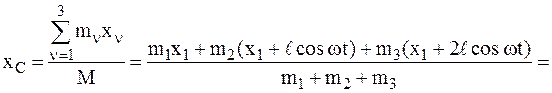
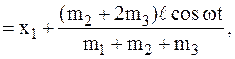
здесь 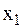 – перемещение мотора (переменная величина),
– перемещение мотора (переменная величина),
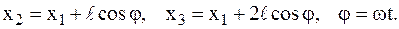
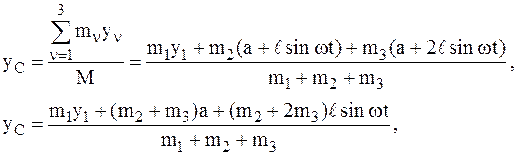
здесь
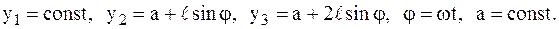
5 1-я задача динамики – определить силу реакции фундамента  (используется проекция на ось у).
(используется проекция на ось у).
 6а К01 КМТ
6а К01 КМТ

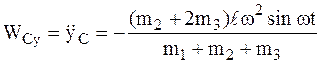
7а 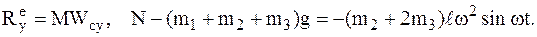
8а 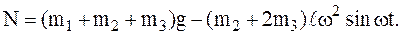
Ответ: 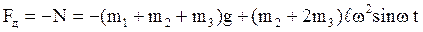
Мотор будет подпрыгивать над фундаментом, если 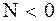 ,
,
т.е. при 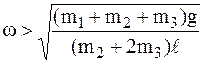 ,
, 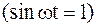 .
.
9а 2-я задача динамики – определить горизонтальное перемещение 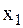 мотора (используется проекция на ось х).
мотора (используется проекция на ось х).
5 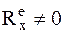 .
.
6в 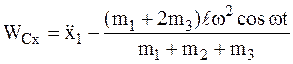

7в 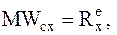
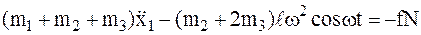 .
.
Подставляется 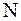 из 8а и определяется
из 8а и определяется 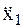 :
:
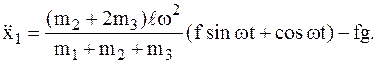
8в Дважды интегрируется предыдущее уравнение
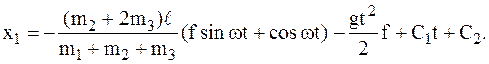
Постоянные интегрирования определяются с помощью начальных условий:
при t = 0 x = 0, следовательно, 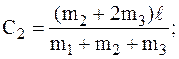
при t = 0 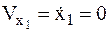 , следовательно,
, следовательно, 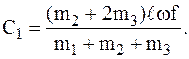
9в Ответ: 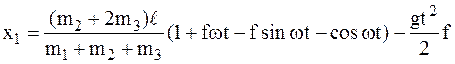 .
.
Пример 2
2 Три тела массы 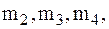 соединенные нерастяжимой нитью, переброшенной через неподвижные блоки, находятся на трапеции массы
соединенные нерастяжимой нитью, переброшенной через неподвижные блоки, находятся на трапеции массы 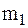 (рис. 32)
(рис. 32)
Определить перемещение трапеции относительно пола, если тело массы 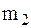 опустится вниз на h. Трением скольжения и массами блоков и нити пренебречь.
опустится вниз на h. Трением скольжения и массами блоков и нити пренебречь.
В начальный момент времени трапеция и тела находятся в покое. Ось х горизонтальна, ось у проходит через положение центра масс трапеции в начальный момент времени.
МС состоит из: АТТ (усеченной пирамиды) и трех МТ.
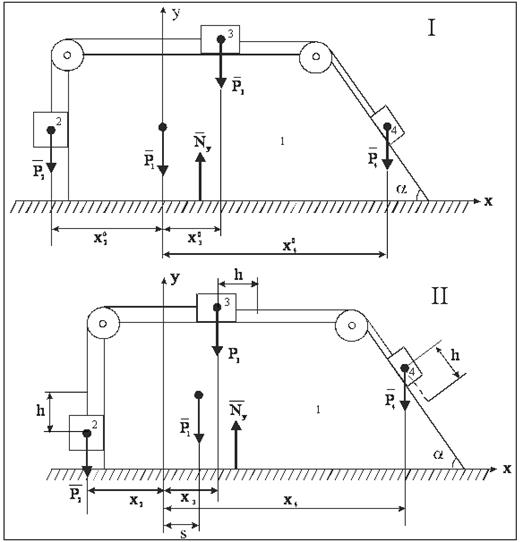
Рис. 32
 3С04 ППВ
3С04 ППВ
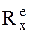
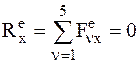 .
.
4 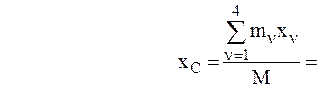
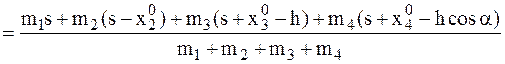 .
.
Здесь 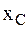 – абсцисса центра масс МС после того, как МТ массы
– абсцисса центра масс МС после того, как МТ массы 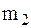 опустится на h. Абсциссы трех МТ для указанного момента времени записываются с учетом того, что эти МТ участвуют в сложном движении (переносное перемещение вместе с трапецией на s и относительное перемещение этих МТ относительно трапеции).
опустится на h. Абсциссы трех МТ для указанного момента времени записываются с учетом того, что эти МТ участвуют в сложном движении (переносное перемещение вместе с трапецией на s и относительное перемещение этих МТ относительно трапеции).
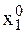 - абсцисса центра масс трапеции, а
- абсцисса центра масс трапеции, а 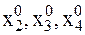 – координаты МТ в начальный момент времени.
– координаты МТ в начальный момент времени.
5 2-я задача динамики – определить s (используются проекции на ось x).
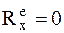 ,
, 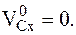
6б 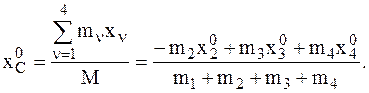
7б 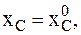
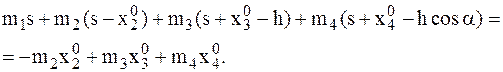
9 Ответ: 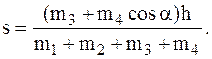
Дата добавления: 2016-06-05; просмотров: 2865;











