Сложное движение точки

Во многих задачах движение точки приходится рассматривать относительно двух (и более) систем отсчета, движущихся друг относительно друга. Такое движение точки является сложным движением. В простейшем случае сложное движение состоит из относительного и переносного движений.

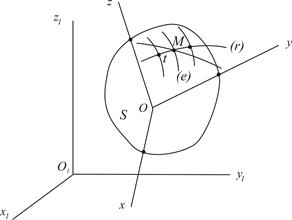
Рисунок 2.27

Пусть имеем две системы отсчета, движущиеся друг относительно друга. 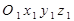- неподвижная или основная система отсчета, 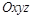- подвижная система отсчета, жестко скрепленная с телом S (рис.2.27). Движение точки относительно подвижной системы отсчета 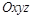называется относительным. Характеристики этого движения называются относительными. Их обозначают индексом r; для скорости и ускорения 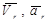. Движение точки относительно основной или неподвижной системы отсчета 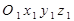, называется абсолютным (или сложным). Траектория, скорость и ускорение этого движения называются абсолютными. Скорость и ускорение абсолютного движения обычно обозначают буквами 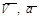без индексов. Переносным движением точки называют движение, которое она совершает вместе с подвижной системой отсчета, как точка жестко скрепленная с этой системой в рассматриваемой момент времени. В следствии относительного движения движущаяся точка в различные моменты времени совпадает с различными точками тела S, с которым скреплена подвижная система отсчета. Переносной скоростью и переносным ускорением являются скорость и ускорение той точки тела S, с которой в данный момент совпадает движущаяся точка. Переносная скорость и переносное ускорение обозначают .

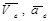Абсолютная и относительная (локальная) производная вектора. Формула Бура. Для любого вектора 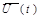его производную по времени по отношению к неподвижной системе отсчета называют полной (или абсолютной) производной и обозначают 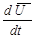. Производную по времени при учете изменения вектора 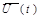относительно подвижной системы отсчета называют относительной (или локальной) производной и обозначают 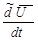. Введем неподвижную систему координат 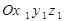. Подвижная система координат 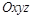вращается вокруг мгновенной оси с угловой скоростью 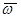. Поступательное движение подвижной системы координат не учитывается, так как это не изменяет вектор .

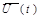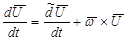(2.36)

Это формула Бура зависимости производных вектора 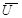в двух системах отсчета, движущихся друг относительно друга.