Пример расчета скоростей и ускорений точек при сложном движении

Определить абсолютную скорость и абсолютное ускорение точки М (рис.2.30) в момент времени t₁=1 c.

Решение. Движение точки М можно рассматривать как сложное, то есть как сумму двух движений: переносное вращение вместе с пластиной и относительное перемещение по дуге АМ. Тогда абсолютную скорость и абсолютное ускорение можно найти по формулам

,

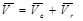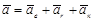
где 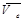- переносная скорость точки,

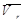- относительная скорость точки,

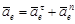- переносное ускорение точки,

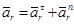- относительное ускорение точки,

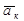- - ускорение Кориолиса

Определим все характеристики относительного и переносного движения. Относительным движением является движение по дуге окружности, которое происходит по закону

(2.48)

Полагая в уравнении (2.48) t=1 c, получим

.

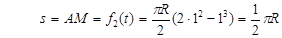Рисунок 2.30

Точка М лежит на вертикальном диаметре круглой пластины (рис. 2.30).

Расстояние от точки М до оси вращения О определяем по формуле

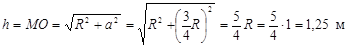(2.49)

Теперь находим характеристики относительного движения точки М

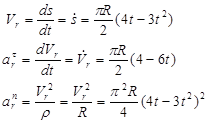(2.50)

Для момента времени t₁=1 с и R=1 м получим

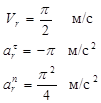(2.51)

Направление векторов показано на рисунке 2.30.

Переносным движением является движение точки круглой пластины, совпадающей в данный момент с точкой М, при ее вращении вокруг оси, проходящей через точку О, и перпендикулярной плоскости чертежа. Найдем алгебраические значения угловой скорости и углового ускорения переносного вращения в данный момент времени

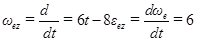(2.52)

Для момента времени t₁=1 с получим

.

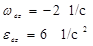Знак «минус» перед угловой скоростью означает, что пластина вращается в направлении противоположном направлению угла φ, указанному на рис. 2.30 стрелкой. Численные значения угловой скорости и углового ускорения соответственно равны

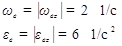
Зная угловую скорость и угловое ускорение, можно определить численные значения переносной скорости и ускорения точки М

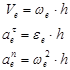(2.53)

Для момента времени t₁=1 с , учитывая значения параметров и при R=1м получим

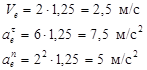
Вектор переносной скорости направлен перпендикулярно радиусу вращения МО в сторону дуговой стрелки угловой скорости 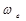Нормальная составляющая переносного ускорения направлена к центру переносного вращения, то есть к точке О, а касательная составляющая направлена перпендикулярно радиусу вращения МО в сторону дуговой стрелки углового ускорения .

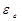Вектор переносной угловой скорости направлен по оси вращения таким образом, что с его конца вращение наблюдается против часовой стрелки. В нашем случае вектор угловой скорости направлен перпендикулярно плоскости чертежа и смотрит на нас.

Модуль ускорения Кориолиса определяется по формуле

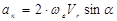(2.54)

где α – угол между вектором переносной угловой скорости и вектором относительной скорости точки М. В нашем случае α=90⁰. По формуле (2.54) численно получим

.

Направление ускорения Кориолиса определяем по правилу Жуковского. В нашем случае плоскость перпендикулярная оси переносного вращения совпадает с плоскостью пластины и проекция вектора на эту плоскость совпадает с самим вектором 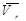. Поворачивая 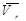на 90⁰ по направлению 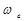получаем направление 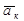(рис.2.30).

Для того, чтобы определить значения абсолютной скорости и абсолютного ускорения точки М, используем метод проекций, выберем ортогональную систему координат. Ось Мx направим по вектору 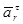, ось Мy – по вектору 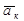. Третья ось Мz в данной задаче не требуется, так как все составляющие скорости и ускорения лежат в плоскости Мxy.

Проецируем все составляющие вектора скорости на координатные оси Мx и Мy :

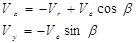
Абсолютную скорость вычисляем по теореме Пифагора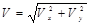

учитывая, что

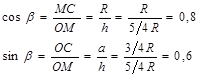
получим при t₁=1 с

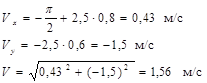
Для абсолютного ускорения аналогичным образом получим

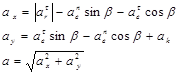при t₁=1с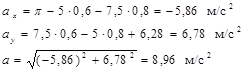

ДИНАМИКА

В динамике изучается механическое движение материальных объектов с учетом их взаимодействия с окружающими материальными тела и средой, т.е. с учетом сил, действующих на эти объекты. Из статики в динамику переносят аксиому освобождения от связей точек системы, теорию сложения сил и приведения систем сил к простейшему виду, из кинематики — методы и приемы описания движения и запись уравнений связей.