Уравнения деформации конструкции

Для определения деформации в горизонтальном направлении вводим добавочную силу P_д, тогда:

,

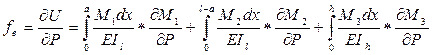
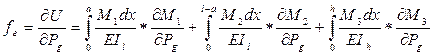где Е-модуль упругости

I_l,I_h - моменты инерции соответственно горизонтального и вертикального звеньев,

М₁; М₂; М₃-изгибающие моменты в сечениях x₁, x₂ ,x₃

_{; ; ;}

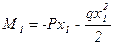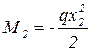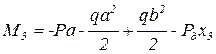Подставляя, полученные выражения в исходные формулы, и принимая, Р_д=0, получаем:

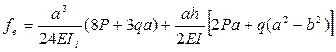
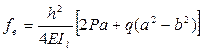
Из формул следует, что прогиб горизонтально расположенного плеча в вертикальном направлении вызван деформацией горизонтальной и вертикальной стоек, а смещение плеча в горизонтальном направлении обусловлено только деформацией вертикальной стойки.

Влияние некоторых конструктивных параметров на величину деформации, рассмотрено при максимальном вылете плеча a=l, то есть при максимальной деформации системы. Так при одинаковой длине вертикальной и горизонтальной стоек системы l=h и одинаковой их жесткости I_l=I_h, формулы прогибов принимают вид:

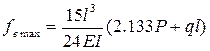
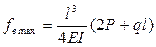
Сравнивая эти деформации, при принятых условиях получим, что деформации в вертикальном направлении более чем в 2,5 раза больше, чем в горизонтальном

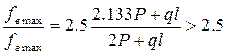
Учитывая то, что деформации в вертикальном направлении складываются из деформации вертикальной и горизонтальной стоек, формулу прогиба в данном направлении можно записать:

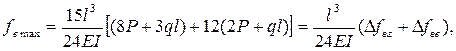
где 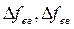- составляющие , учитывающие влияние соответственно горизонтальной и вертикальной стоек на деформацию в вертикальном направлении. При сравнении этих составляющих получим, что прогиб в вертикальном направлении более чем в 3 раза зависит от деформации вертикальной стойки, чем от горизонтальной:

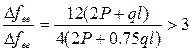
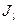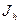Уже из этих сравнений следует, что жесткость вертикальной стойки должна быть значительно выше горизонтальной. Соотношение деформаций системы в вертикальном и горизонтальном направлениях, при различных соотношениях длин l и h и жесткостей и приведено на рис. 42. На этом же рисунке приведены графики, показывающие влияние деформаций вертикального и горизонтального звеньев на прогиб в вертикальном направлении. Эти графики позволяют правильно подобрать соотношение жесткостей этих звеньев для обеспечения минимальных прогибов системы. Приближенно можно рекомендовать для конструкций, в которых длина горизонтального звена меньше длины вертикального, чтобы жесткость вертикального звена была в 4-5 раз больше, чем у горизонтального. При короткой вертикальной стойке по отношению к горизонтальному звену, ее жесткость должна быть выше последнего в 2-3 раза. Зная допустимую величину прогиба в любом направлении, и определив оптимальное соотношение жесткостей вертикального и горизонтального звеньев из графиков (рис. 42) по формулам для 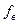и 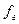, можно определить размеры их сечений.

Аналогичным путем можно оценить влияние отдельных звеньев на суммарную деформацию конструкции при других направлениях действующих нагрузок.