Уравнения движения механизма

Для механизмов с несколькими степенями свободы при голономных связях (все геометрические связи и те дифференциальные связи, уравнения которых могут быть проинтегрированы) уравнения движения составляют в форме уравнений Лагранжа второго рода:

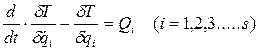
где Т – кинетическая энергия механизма (системы);

s – число обобщенных координат, которое совпадает с числом степеней свободы;

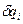- обобщенные координаты;

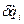- обобщенные скорости;

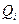- обобщенные силы, каждая из которых есть скалярная величина, равная отношению суммы возможных работ сил, приложенных к механической системе, при изменении только данной обобщенной координаты, к вариации этой координаты. Для обобщенной координаты, имеющей размерность длины, соответствующая ей обобщенная сила имеет размерность силы, а для обобщенной координаты, выраженной в радианах – размерность момента сил.

Обобщенную силу, имеющую размерность момента сил, называют обобщенным моментом сил. В механизмах с одной степенью свободы обобщенная сила совпадает с приведенной силой, а обобщенный момент сил – с приведенным моментом пар сил.

Обобщенные силы определяются из выражения

,

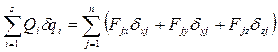где 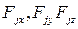- проекции внешних сил 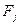на координатные оси x, y, z;

dx_j, dy_j, dz_j - проекции возможных перемещений точек приложения этих сил на оси x, y, z, равные вариациям координат этих точек.

Для функции, зависящей от времени t и аргументов x_i, вариацией называется изменение функции при бесконечно малых изменениях аргументов x_i и фиксированном значении времени t.

Составление уравнений движения рассмотрим на примере манипулятора с числом степеней свободы W=7 (рис. 34).

Полагаем, что внешние силы 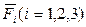, действующие на звенья 1, 2, 3 дают пары с моментами 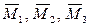. За обобщенные координаты принимаем углы поворота звеньев 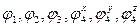и перемещение 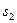. Тогда уравнения движения манипулятора запишутся:

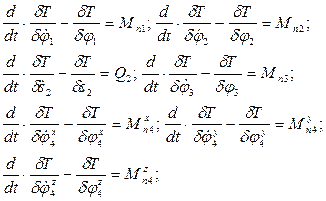
Где 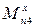, , 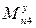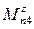- приведенные моменты сил относительно осей неподвижной системы координат.

Кинетическая энергия звеньев манипулятора при условии, что центробежные моменты инерции обратятся в нуль:

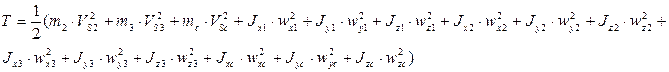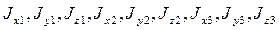где - моменты инерции звеньев относительно осей, проходящих через центры масс звеньев;

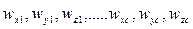- проекции на координатные оси мгновенной угловой скорости звеньев при сферическом движении вокруг центра масс.

Для нахождения уравнения движения манипулятора необходимо осуществить дифференцирование выражения кинетической энергии по переменным 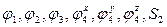, а затем по времени t.

Составление уравнений

Движения

За обобщенные координаты (рис. 35) примем цилиндрические координаты, определяющие положение центра масс захвата с грузом 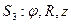. Кинетическая энергия робота при неподвижном основании и уравновешенном звене 1 определяется как:

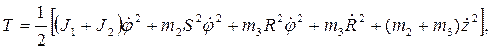
где 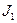- момент инерции звена 1 относительно оси z;

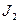- момент инерции звена 1 относительно оси, проходящей через центр масс 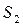параллельно оси z₁;

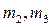- массы звеньев 2 и 3;

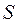- расстояние от оси z до центра масс звена 2.

Уравнения движения запишем в форме:

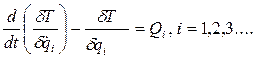
Где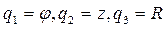

При определении обобщенных сил 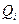считаем, что поступательные приводы звеньев 2 и 3 (например, гидроцилиндры) расположены на подвижных звеньях и создают движущие силы 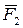и 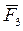, а вращательный привод звена 2 создает движущий момент пары сил 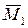. Кроме того учитываем силы тяжести звеньев 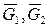и силы трения 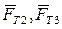в парах 1-2, 2-3. Силы трения и момент сил трения во вращательной паре считаем постоянными и известными из опытных данных. Для случая движения звена 2 вверх и звена 3 от оси z имеем:

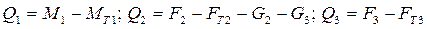
Выполняя дифференцирование и подставляя значения обобщенных сил, получаем уравнения движения:

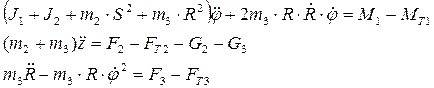
Закон изменения координаты z находится непосредственно из уравнения, а для определения координат 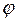и 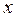имеем систему двух нелинейных дифференциальных уравнений второго порядка, которая обычно решается численными методами на ЭВМ.

При цикловом управлении роботом часто перемещают захват сначала изменением координаты 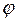, а затем координаты R (или наоборот). Из уравнений движения следует, что изменение координаты 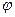вызывает одновременно изменение координаты R. Во избежание взаимодействия и взаимовлияния движения по координатам 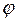и R применяют фиксирующие устройства в заданных конечных положениях звеньев манипулятора.