Определение усилий приводов манипулятора при реализации движения объекта по заданной траектории

Задачи данного типа относятся к классу так называемых обратных задач динамики, сводящихся к решению обратных задач теории дифференциальных уравнений. Решение обратных задач динамики манипуляторов позволяет в различных постановках решать вопросы их проектирования и управления.

Кинематическая схема манипулятора приведена на рис. 36. Звено 1 выполняет поворот на угол 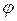вокруг вертикальной оси z, звено 2 – вертикальное перемещение, звено 3 – горизонтальное перемещение.

Пусть необходимо обеспечить движение захвата манипулятора по эллиптической траектории с заданным законом изменения скорости.

Траекторию движения захвата задаем как линию перемещения цилиндрической поверхности и плоскости:

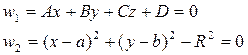
А закон изменения скорости функцией:

,

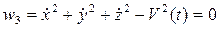где 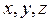- декартовы координаты захвата,

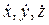- проекции вектора скорости на эти оси.

Для получения дифференциальных уравнений движения данной схемы механической системы воспользуемся методом Лагранжа. За обобщенные координаты примем 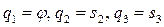. Тогда уравнения Лагранжа примут вид:

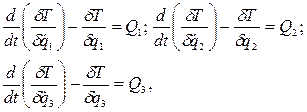
где 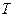- кинетическая энергия системы в ее абсолютном движении,

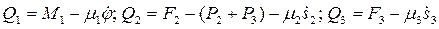- обобщенные силы, соответствующие обобщенным координатам ;

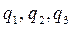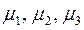- коэффициенты вязкого трения;

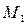- момент привода 1,

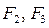- усилия приводов звеньев 2 и 3.

Тогда уравнения можно записать:

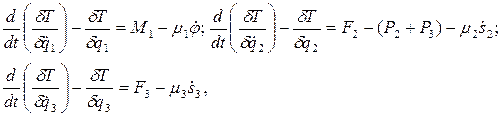
где 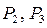- вес звеньев 2 и 3.

Кинетическая энергия манипулятора

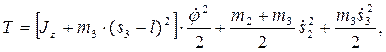
где 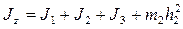, а 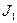- момент инерции звена 1, 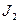и 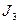- моменты инерции звеньев 2 и 3 относительно их центральных осей, параллельных оси вращательной пары,

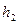- расстояние центра масс звена 2 от его оси вращения,

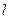- расстояние захвата от центра масс звена 3.

Дифференциальные уравнения движения системы в обобщенных координатах имеют следующий вид:

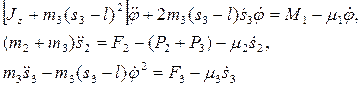
Декартовы координаты точек траектории и проекции скорости на эти оси через обобщенные координаты выражаются следующим образом:

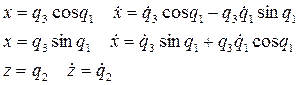
Тогда функции 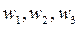, выражающие заданные свойства движения системы, в обобщенных координатах примут вид:

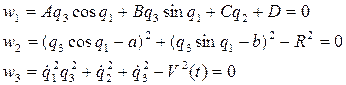
Как следует из общего решения обратных задач динамики, для того, чтобы система дифференциальных уравнений описывала движение механизма с заданными свойствами, которые выражаются функциями 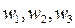необходимо и достаточно, чтобы полные производные по времени от этих функций равнялись нулю и чтобы начальное состояние системы также удовлетворяло этим заданным свойствам.

Учитывая, что частные производные 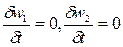, то получим:

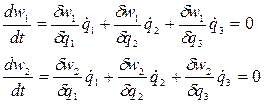(54)

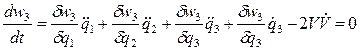(55)

Дифференцируя (54) по времени и объединяя с (55), получим неоднородную систему трех алгебраических линейных уравнений относительно :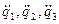

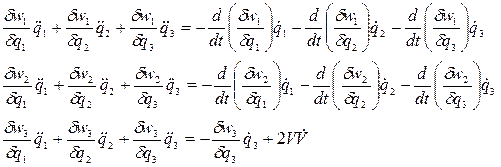
Задание законов изменения скорости или касательного ускорения захвата манипулятора при его движении по траектории позволяет однозначно определить 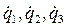. Далее решая систему трех уравнений определяются 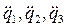. Зная координаты, скорости и ускорения захвата из уравнений Лагранжа можно определить 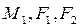, которые должны развивать приводы для осуществления заданного движения захвата манипулятора.

Знание этих сил позволяет построить алгоритм управления движением промышленного робота по заданной программе.