Определение сил и моментов, обеспечивающих программное движение манипулятора

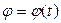Манипулятор (рис. 37), состоящий из звеньев 1, 2 и захвата D, приводится в движение приводами A, B. Захват D перемещается вдоль прямой ON. Со стороны привода A к звену 1 приложен управляющий момент M₁. Привод B воздействует на звено 2 управляющим усилием P₂. Перемещение звена 1 ограничено препятствиями K и L, поэтому изменение угла поворота этого звена возможно лишь в интервал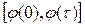е , где 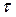- время движения звена. Технические условия работы манипулятора требуют, чтобы указанное звено сошло со связи K при t=0 и “мягко” коснулось препятствия L при t= 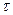, то есть так, чтобы были удовлетворены условия:

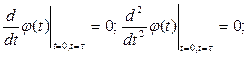
Программное движение звена 1, удовлетворяющее требованиям “мягкого” касания задано в виде:

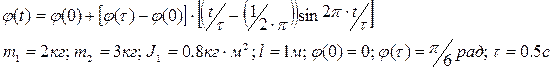
Необходимо найти управляющий момент М и управляющую силу Р.

Рассматривая манипулятор как механическую систему с двумя степенями свободы принимаем за обобщенные координаты угол 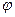поворота звена 1 и перемещение x звена 2.

Для рассматриваемой механической системы:

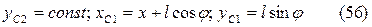
Эти равенства выполняют роль уравнений связей. В соответствии с выбранными обобщенными координатами:

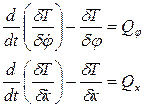(57)

Совокупность уравнений (56) и (57) позволяет составить дифференциальные уравнения движения механической системы.

Составим выражения для кинетической энергии системы, которая складывается из кинетической энергии звена 1 и кинетической энергии звена 2:

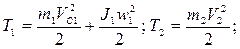
где , .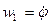

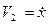Продифференцировав (56) по времени:

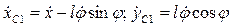, откуда

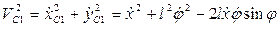
Найдем значения слагаемых уравнений Лагранжа:

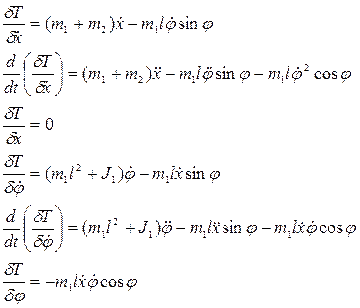
Определим обобщенные силы 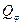и .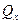

Для определения 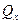мысленно наложим на систему связь 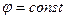и сообщив возможное перемещение 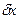по обобщенной координате определим работу сил:

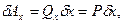таким образом, 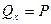. ( 58)

То же самое проделаем для определения обобщенной силы .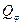

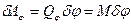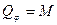, а (59)

Подставляя результаты, получим

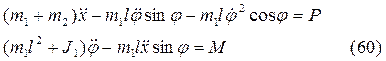
Так как захват манипулятора по условию задачи должен перемещаться вдоль прямой, перпендикулярной оси x, на механизм дополнительно оказывается наложенной связь

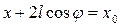или

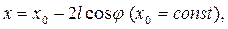
Следовательно

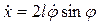, а

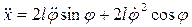(61)

Подставив (61) в (60) получим

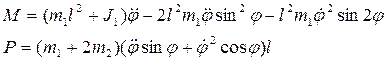(62)

Равенства (62) представляют собой зависимость управляющего момента М и управляющего усилия Р от известных функци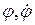й и 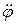. Так как 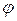является заданной функцией времени, то вычисление производных 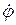и 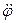возможно. В момент торможения угловое ускорение обращается в нуль.

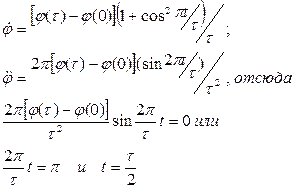
Таким образом, торможение звена 1 начинается в момент времени 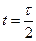. В этот момент времени

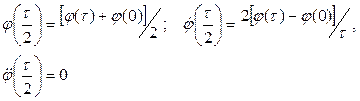(63)

Подставляя (63) в (62), получим

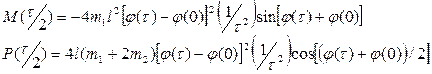
Учитывая условия задачи, получаем

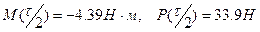
Приведя вычисления в интервале 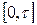с шагом 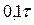, строим графики зависимостей М и Р от времени (рис. 38)