Вычисление определителя матрицы

И построение обратной матрицы

Вычисление определителя

Используя схемы исключения (Гаусса и др.), можно вычислить определитель квадратной матрицы 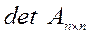. Поскольку для треугольной и диагональной матриц определитель равен произведению элементов главной диагонали, то при использовании методов Гаусса и Жордана определитель можно получить, перемножив ведущие элементы, определявшиеся в процессе выполнения прямого хода этих методов:

,

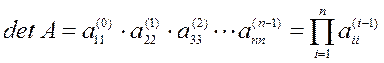где верхний индекс – номер шага.

Если на каком–то шаге процесса ведущий элемент 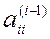= 0 или близок к нулю, то следует переставить столбцы или строки матрицы 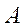так, чтобы на главной диагонали стоял ненулевой элемент. В итоге

,

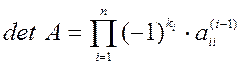где k_i для i–го шага вычисляют по формуле:

k_i =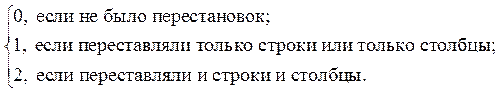

Для вычисления определителя с использованием схем исключения требуется 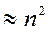ячеек памяти и 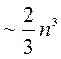арифметических операций, что значительно меньше, чем при вычислении определителя по всевозможным произведениям элементов.

Задача

Вычислить определитель матрицы A, используя метод Гаусса:

A= .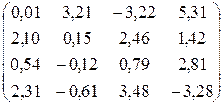

Решение. Поскольку 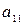близко к нулю, используем схему с выбором главного элемента (см. п. 4.1.2).

i = 1. Главный элемент 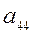= 5,31. Поменяем местами 1–й и 4–й столбцы, чтобы этот элемент стал ведущим, затем вынесем ведущий элемент за знак определителя и получим нули в первом столбце матрицы под диагональным элементом:

.

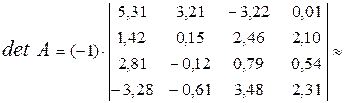
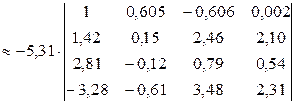
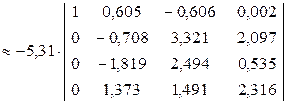i = 2. Главный элемент 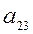= 3,321. Поменяем местами 2–й и 3–й столбцы, затем вынесем ведущий элемент за знак определителя и получим нули во втором столбце матрицы под диагональным элементом:

.

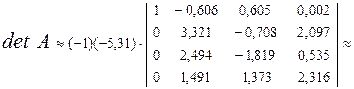
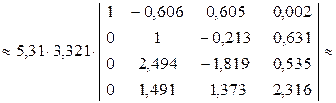
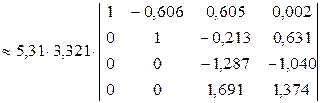i = 3. Ведущий элемент 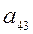= 1,691. Поменяем местами 3-ю и 4-ю строки, затем вынесем ведущий элемент за знак определителя и получим ноль под ним:

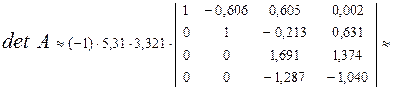
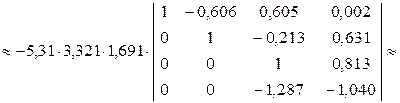
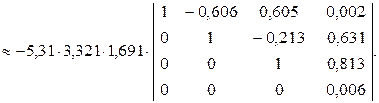
i = 4. Выносим за знак определителя последний ведущий элемент:

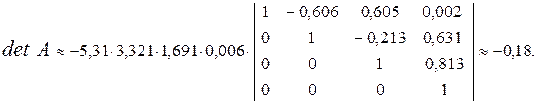
Ответ: 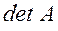= -0,18.