Классификация систем

Рассмотрим систему линейных алгебраических уравнений

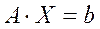(1)

где 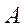– матрица размерности ;

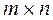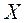– вектор размерности ;

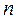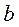– вектор размерности .

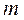Система (1) совместна, если ранги матрицы 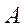и расширенной матрицы 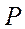= ( 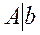), полученной из 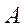присоединением столбца 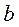, совпадают: 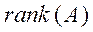= 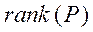. Если система (1) несовместна, то ставится задача нахождения обобщенного решения 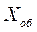, которое дает минимум функции невязок

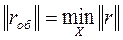, (2)

где .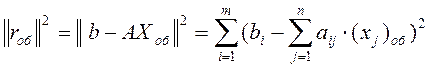

(Здесь и далее рассматривается евклидова норма вектора).

Возможны 4 случая при решении системы (1).

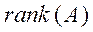
1. 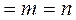. Совместная система с невырожденной квадратной матрицей 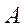, она имеет единственное решение 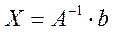, которое можно найти, используя прямые или итерационные методы.

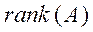
2. 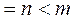. Переопределенная система (число уравнений больше числа неизвестных). Если система несовместная, ставится задача отыскания обобщенного решения 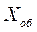, минимизирующего функцию (2). В случае совместности системы это решение оказывается обычным решением.

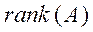
3. 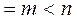. Неопределенная система, имеет бесконечно много решений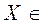 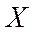. Ставится задача отыскания нормального решения 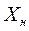, имеющего наименьшую норму

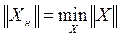. (3)

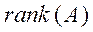
4. 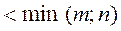. Вполне неопределенная система. Если она совместна, то имеет бесконечно много решений, а если несовместна, то может иметь бесконечно много обобщенных решений 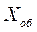. Ставится задача отыскания обобщенного нормального решения, имеющего наименьшую евклидову норму среди всех решений, доставляющих минимум функции (2), те

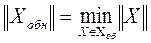. (4)

7.2 Нахождение обобщенного решения переопределенной системы с помощью первой трансформации Гаусса

Рассмотрим систему

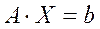(1)

в случае, когда 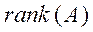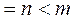(размерность матрицы – ).

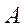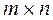Осуществляем 1–ю трансформацию Гаусса: умножим (1) на транспонированную матрицу 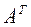слева, получим:

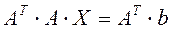. (5)

Здесь (5) – система вида 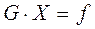с квадратной матрицей 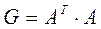размерности ( ), невырожденной, симметричной. Решение системы (5) 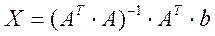(его можно получить, используя прямые или итерационные методы) – это обобщенное решение системы (1), оно дает минимум нормы вектора невязок среди всех возможных решений.

Задача 1

Найти обобщенное решение переопределенной системы при помощи 1–ой трансформации Гаусса. Точность вычислений 0,01.

.

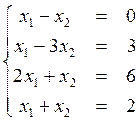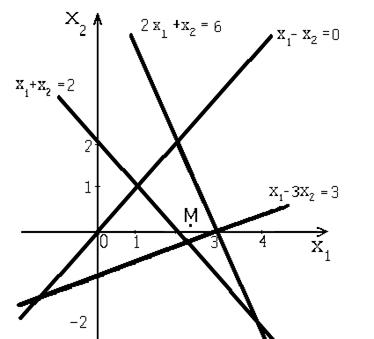
Решение. Сделаем геометрическую иллюстрацию задачи: даны 4 прямые на плоскости 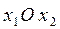.Требуется найти точку 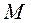, для которой выполнялось бы условие (2).

Введем обозначения:

;

; .

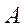
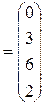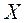
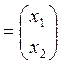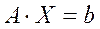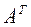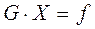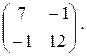
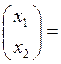
Тогда систему можно записать так: . Умножим обе части уравнения на матрицу слева, получим или: 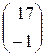. Здесь , .

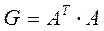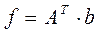Тогда = .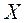

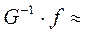
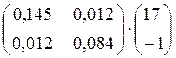
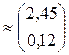Норма вектора невязок сильно отличается от нуля: 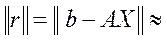7,54, однако, это - минимум, который может быть достигнут для данной системы, т.е. получены координаты точки М (см. рисунок).

Ответ: обобщенное решение системы 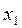= 2,45; 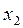= 0,12.

Задача 2

Найти обобщенное решение переопределенной системы при помощи 1–ой трансформации Гаусса и метода Зейделя. 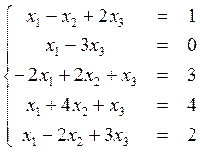. Точность вычислений 0,001.

Решение. Введем обозначения:

; ; .

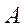
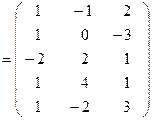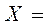
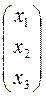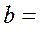
Применяем 1–ю трансформацию Гаусса: 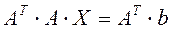, или

.

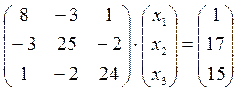Это система уравнений с квадратной матрицей вида 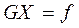. Решим эту систему методом Зейделя с точностью до 0,001 (см. §5, п.5.2). Для этого построим матрицу :

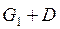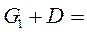
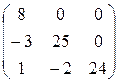
Возьмем начальное приближение 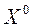= (0; 0; 0)^T, , для него вектор невязок 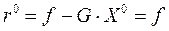. Дальнейшие расчеты занесем в таблицу.

k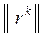
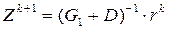
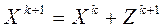
	22,6936	(0,125; 0,695; 0,6778)T	(0,125; 0,695; 0,6777)T
	1,9539	(0,1759; 0,0753; –0,0010)T	(0,3009; 0,7703; 0,6767)T
	0,2270	(0,0284; 0,0033; –0,0009)T	(0,3293; 0,7736; 0,6758)T
	0,0110	(0,0014; 0,0001; –0,0000)T	(0,3307; 0,7737; 0,6757)T
	0,0003

Поскольку 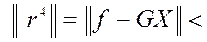0,001, вычисления прекращаем. Полученный вектор 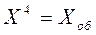- обобщенное решение исходной системы. Норма вектора невязок исходной системы 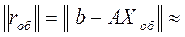2,526.

Ответ: обобщенное решение системы = 0,331; 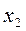= 0,774; 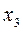= 0,676.

7.3 Нахождение нормального решения неопределенной

системы с помощью второй трансформации Гаусса

Требуется решить систему 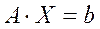(1) с матрицей 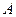размерности 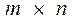, причем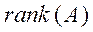 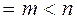(неопределенная система). Используем 2–ю трансформацию Гаусса: заменяем 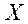на произведени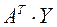е , где 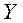– вектор размерности 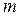: 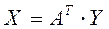, тогда (1) можно записать в виде

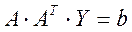. (6)

Здесь (6) - система вида 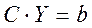с квадратной матрицей 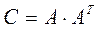размерности , неособенной, симметричной. Решение системы (6) можно получить, используя прямые или итерационные методы: 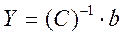. Тогда нормальное решение системы (1):

.

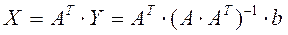Это решение имеет наименьшую норму среди всех возможных решений системы.

Пример. Система двух уравнений с тремя неизвестными:

.

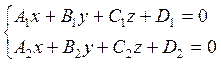Геометрически решения этой системы - это множество общих точек двух плоскостей в пространстве. Если это множество не пусто (плоскости не параллельны), то таких точек бесконечное множество (прямая либо плоскость). Нормальное решение системы - это точка, радиус-вектор которой имеет наименьшую норму среди всех возможных решений, т.е. точка, наиболее близкая к началу координат в пространстве решений.

Задача

Найти нормальное решение неопределенной системы при помощи 2–ой трансформации Гаусса. Точность вычислений 0,01

.

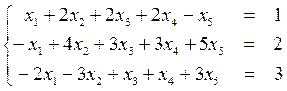Решение. Обозначим ; ; .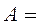

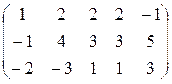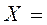
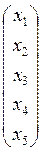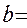
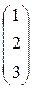В системе уравнений 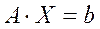сделаем замену 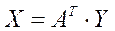, получим систему с квадратной матрицей :

. .

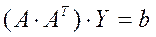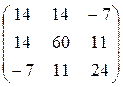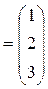Используя прямые или итерационные методы, получаем решение этой системы:

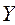= (0,256; -0,068; 0,231)^T .

Теперь находим нормальное решение исходной системы – вектор 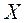, имеющий наименьшую норму среди всех решений исходной системы:

.

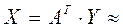
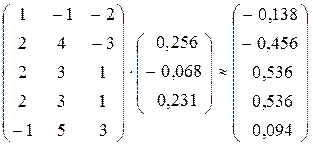Норма вектора невязок для полученного нормального решения: 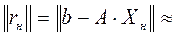0,002.

Ответ: нормальное решение системы

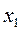= -0,14; 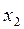= -0,46; 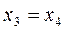= 0,54; 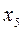= 0,10.

В заключение можно отметить существенный недостаток обеих трансформаций Гаусса: они ухудшают обусловленность системы.

Литература

Конспект лекций.