Метод сопряженных градиентов

Дана система уравнений

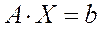,(1)

где 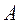-симметричная положительно определенная матрица (невырожденная).

Решение этой системы может быть найдено при помощи метода сопряженных градиентов. В процессе работы метода сопряженных градиентов строится система 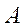- сопряженных векторов 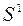, , 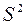..., 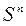, т.е. векторов, удовлетворяющих для 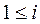, 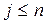условиям:

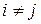, если ;

, если .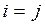

Собственно схема решения системы (1) с использованием векторов следующая. Строится последовательность , , ... , где 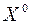произвольный вектор, таким образом, что перемещение от 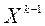к осуществляется в направлении вектора , 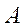-сопряженного к каждому из уже построенных ранее векторов 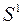, , ..., . 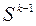Метод сопряженных градиентов относится к прямым методам, т.к. не позднее, чем на 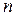–ом шаге процесса (n - размерность системы) в предположении отсутствия округлений будет построено точное решение системы линейных уравнений . Но поскольку решение с точностью >0 нередко удается получить раньше ( ), то этот метод используется как итерационный. Критерий остановки расчетов: , где 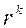– вектор невязки. Система векторов 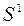, , 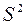... строится одновременно с последовательным нахождением , , ... .

Описание алгоритма.

1) Берем произвольный вектор 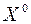, например 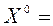(0; ...0)^T, вычисляем . Выбираем 1–е направление .

2) Для 1, 2, ... n, или пока не будет выполнено вычисляем

; ; ;

; .

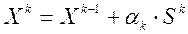Последний полученный вектор 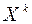принимается за искомое решение системы линейных уравнений (1).

Формулы для вычислений даны в предположении, что матрица – симметричная. Если это не так, то можно, например, перейти от решения системы (1) к решению системы .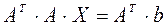

Метод сопряженных градиентов эффективен, если размерность 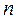велика, поскольку часто удается получить решение системы с заданной точностью при числе итераций .

Если за 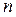шагов не удалось получить решение с заданной точностью, следует изменить 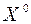и повторить весь процесс решения сначала.

Задача

Решить систему из п.5.3 методом сопряженных градиентов. Точность = 0,01.

Решение. Пусть 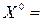(0; 0; 0; 0)^T. Тогда 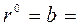(1,34; 0,85; 1,29; 2,11), 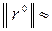2,983, .Дальнейшие расчеты приведены в таблице.

k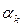
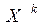
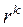
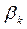
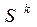
	0,320	0,429 0,272 0,413 0,675	0,102 -0,792 -0,388 0,491	1,014	0,119	0,262 -0,690 -0,234 0,742
	0,306	0,509 0,061 0,341 0,903	-0,085 0,077 -0,084 0,075	0,161	0,025	-0,078 0,059 -0,090 0,093
	0,538	0,467 0,093 0,293 0,953	-0,048 -0,019 0,042 0,012	0,067	0,175	-0,061 -0,009 0,026 0,029
	0,555	0,433 0,088 0,307 0,969

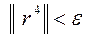, вычисления прекращаем.

Ответ: 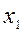= 0,43; 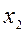= 0,09; 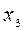= 0,31; = 0,97.

Литература

[1], гл. III, работа №9.

[4], т. II, гл. VI, §5; §10; §11.

[5], гл. II, §2.18–2.19.

[9], гл. VI, §8–10.

Конспект лекций.