Вычисление выборочных характеристик распределения.

Для вычисления среднего значения (математического ожидания, статистики), дисперсии, коэффициентов асимметрии и эксцесса рекомендуется следующий порядок вычислений.

Заменяем интервальный ряд дискретным, для чего все значения признака в пределах интервала приравниваем к его серединному значению, и считаем. Что частота относится к середине интервала. Значения середин интервалов равны .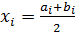

Составляем табл. 3. Значения середин интервалов заносим в графу 1, соответствующие частоты – в графу 2 и т.д. в таблице .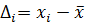

Пользуясь табл. 3, вычислим математическое ожидание:

.

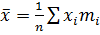В нашем примере 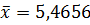мм и характеризует среднее значение наблюдаемого признака.

Выборочный центральный момент k-го порядка равен:

.

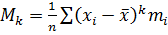Таблица 3

Вспомогательная таблица для вычисления выборочных характеристик

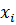
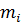
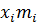
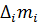
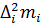
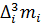
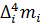
5,03		10,6	-0,8712	0,37949	-0,1653	0,07201
5,14		15,42	-0,9768	0,31805	-0,10356	0,03372
5,25		63,00	-2,5872	0,55780	-0,12026	0,025928
5,36		101,84	-2,0064	0,21188	-0,02237	0,00236
5,47		158,63	0,1276	0,00056	0,00000	0,00000
5,58		100,44	2,0592	0,23557	0,02695	0,00308
5,69		73,97	2,9172	0,65462	0,14690	0,03296
5,80		23,20	1,3376	0,44729	0,14957	0,05002
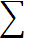
		546,56		2,80526	-0,08808	0,22008

Для проверки правильности вычисления 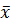используем теорему:

.

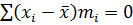В нашем примере теорема выполняется (табл. 3, графа 4).

Для данного примера выборочные центральные моменты равны:

, , .

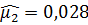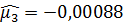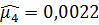Выборочная дисперсия равна центральному моменту второго порядка:

.

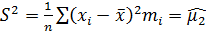В примере 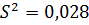, а выборочное среднее квадратическое отклонение 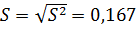мм.

Выборочные коэффициенты асимметрии 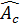и эксцесса 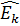определяются по формулам:

; .

, .

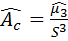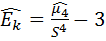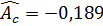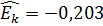Медиана 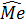– это значение признака 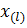, приходящееся на середину ранжированного ряда наблюдений ( 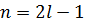). При четном числе наблюдений ( 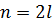) медианой является средняя арифметическая двух значений, расположенных в середине ранжированного ряда:

.

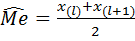Если ранжировать значения, попавшие в медианный интервал 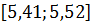, - интервал, в котором накопленная частота 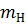впервые превышает половину объёма выборки 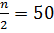, - до значени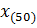й и 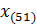, получим

.

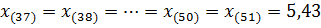Следовательно, 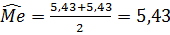мм.

Если исходить из интервального ряда, то медиану следует вычислять по формуле

,

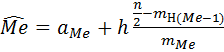где 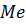означает номер медианного интервала, ( 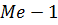) – интервала, предшествующего медианному.

В нашем примере 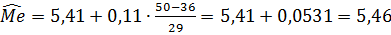мм.

Мода 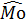для совокупности наблюдений равна тому значению признака (табл. 1), которому соответствует наибольшая частота.

В нашем случае вариант 5,43 имеет наибольшую частоту (m=15). Это означает, что 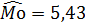мм.

Для одномодального интервального ряда вычисление можно провести по формуле

,

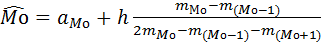где 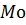означает номер модального интервала (интервала с наибольшей частото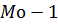й), и 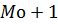- номера предшествующего модальному и следующего за ним интервалов.

В нашем примере

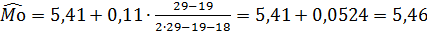мм.

Так как 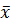, 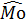и 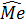почти не отличаются друг от друга, есть основания считать теоретическое распределение нормальным.

Коэффициент вариации .