Построение обратной матрицы методом пополнения

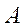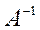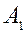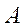
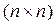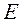
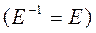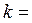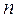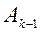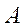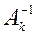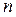Требуется найти обратную матрицу для данной невырожденной квадратной матрицы . За основу построения в методе пополнения берут матрицу той же размерности, что и , но с известной обратной матрицей. Примером такой матрицы может служить единичная матрица . На каждом шаге 1, 2, …, заменяется одна из строк рабочей матрицы строкой матрицы (пополнение) и строится . На –ом шаге получаем 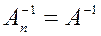. Для пополнения матрицы 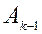используются: вспомогательная строка

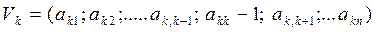(1)

и столбец единичной матрицы 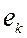= (0; 0; ...1; 0; ..0)^Т. Тогда справедливо: 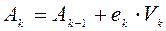, (2)

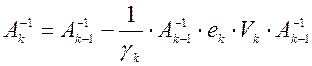и , (3)

где:

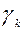– число, определяемое по формуле:

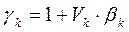, (4)

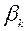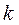- –й столбец матрицы .

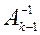Описание одного шага метода пополнения.

1) Пополняем матрицу 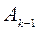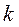–й строкой матрицы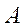

(формула (2)), в результате получаем .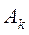

1) Находим 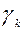– формула (4).

2) Строим матрицу 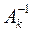по формуле (3) или по столбцам:

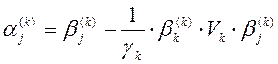, (j = 1, 2, …, 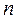), (5)

где 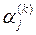– –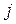й столбец матрицы 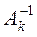(верхний индекс – номер шага).

Метод пополнения удобно использовать в случае, когда известна матрица 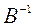, а требуется найти 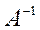для матрицы 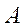, отличающейся от 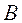несколькими строками.

Задача

Найти матрицу, обратную к матрице 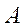из задачи к п.6.2:

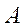
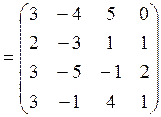. Точность 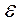= 0,01.

Решение. Пусть , .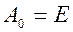

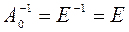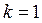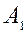
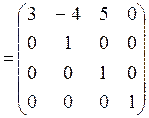
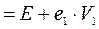. , где

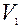= (2;-4;5;0), 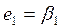= (1;0;0;0)^T; 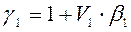=3; 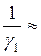0,333;

;

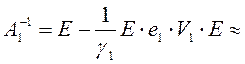
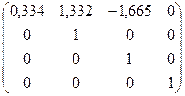Выделим 2-й столбец матрицы 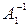: 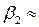(1,332; 1; 0; 0)^T.

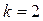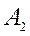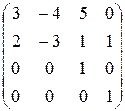
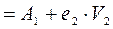. = , где

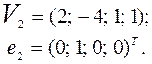
Вычислим

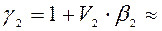
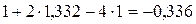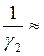; -2,976, тогда

;

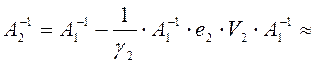
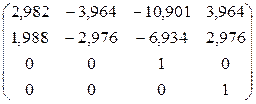Здесь 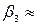(–10,901; –6,934; 1; 0)^T.

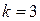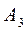
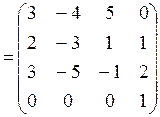
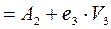. , где

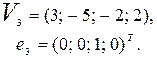
Вычисляем 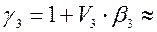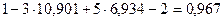; 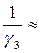1,034;

;

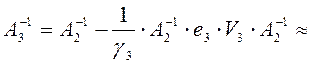
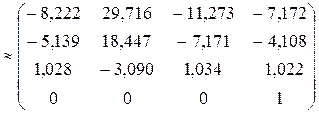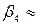(–7,172; –4,108; 1,022; 1)^T.

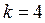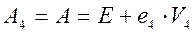. , где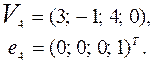

; ;

.

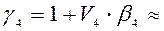
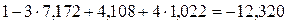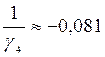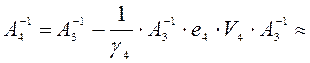
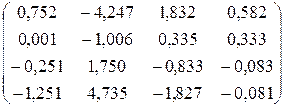Проверив условия 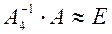, , 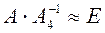убеждаемся в правильности решения.

Ответ: .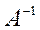

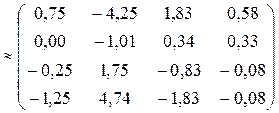Литература

[1], гл. II, работа №2; гл. III, работа №3.

[5], гл. II, §2.6, 2.12.

[8], гл. VIII, п.8.2.2.

Конспект лекций.