Классическая схема Якоби. На каждом шаге выбирают максимальный по модулю недиагональный элемент матрицы : и строят матрицу для обнуления этого элемента.
2. Циклическая схема. Заранее выбирают последовательность, в которой будут строиться матрицы в каждом цикле, например по строкам: T12 , T13 , , . . T1n , затем T23 , Т24 , . . . T2n и т.д. или по столбцам. После завершения цикла его повторяют, пока не будет выполнено .
3. Процесс с преградами. Задают последовательность чисел h1 > h2 > . . ... > hS > 0 . На первом этапе обнуляют те недиагональные элементы матрицы А , которые по модулю больше h1 , когда таких элементов не остается, переходят к следующей «преграде» h2 и т.д.
Если все собственные значения матрицы А различны, то не более, чем за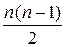 
итераций все недиагональные элементы матрицы будут иметь порядок .
Задача
Найти собственные значения матрицы А из условия задачи 1
п. 8.1. Точность e = 0,01.
Решение: Воспользуемся трехдиагональным видом, к которому удалось привести матрицу А при помощи метода Гивенса и будем считать ее начальным приближением:
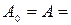
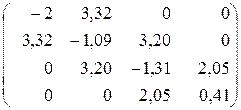
Вычислим = 2×(3,322 + 3,202 + 2,052) = 50,930 > e.. Будем использовать классическую схему метода Якоби. Максимальный по модулю недиагональный элемент а12 = 3,32, поэтому на первом шаге строим матрицу Т12 .
Дальнейшие преобразования матрицы А приведены в таблице. Расчеты проводим с точностью 0,001.
| Номер шага k | i , j , d , c , s | t2(Ak) | |
| i = 1; j = 2 d = 6,702 c = 0,754 s = 0,657 | -4,896 0 -2,104 0 0 1,806 2,411 0 -2,104 2,411 -1,31 2,05 0 0 2,05 0,41 | 28,885 | |
| i = 2; j = 3 d = 5,742 c = 0,878 s = -0,478 | -4,896 -1,006 -1,847 0 -1,006 3,119 0 0,980 -1,847 0 -2,623 1,800 0 0,980 1,800 0,41 | 17,255 | |
| i = 1; j = 3 d = 4,338 c = 0,873 s = -0,488 | -5,929 -0,878 0 0,878 -0,878 3,119 0,491 0,980 0 0,491 -1,590 1,572 0,878 0,980 1,572 0,41 | 10,429 | |
| i = 3; j = 4 d = 3,726 c = 0,877 s = 0,481 | -5,929 -0,878 -0,423 0,770 -0,878 3,119 -0,042 1,095 -0,423 -0,042 -2,453 0 0,770 1,095 0 1,273 | 5,489 | |
| i = 2; j = 4 d = 2,865 c = 0,907 s = -0,422 | -5,929 -0,472 -0,423 1,068 -0,472 3,628 -0,038 0 -0,423 -0,038 -2,453 0,018 1,068 0 0,018 0,763 | 3,088 | |
| i = 1; j = 4 d = 7,025 c = 0,988 s = 0,154 | -6,095 -0,466 -0,420 0 -0,466 3,628 -0,038 -0,073 -0,420 -0,038 -2,453 -0,048 0 -0,073 -0,048 0,930 | 0,805 | |
| i = 1; j = 2 d = 9,768 c = 0,999 s = - 0,048 | -6,117 0 -0,422 -0,003 0 3,651 -0,018 -0,072 -0,422 -0,018 -2,453 -0,048 -0,003 -0,072 -0,048 0,930 | 0,371 | |
| i = 1; j = 3 d = 3,760 c = 0,994 s = -0,113 | -6,165 -0,002 0 -0,009 -0,002 3,651 -0,017 -0,072 0 -0,017 -2,405 -0,047 -0,009 -0,072 -0,047 0,930 | 0,016 | |
| i = 2; j = 4 d = 2,725 c = 1,000 s = 0,027 | -6,165 -0,002 0 -0,009 -0,002 3,653 -0,016 0 0 -0,016 -2,405 -0,048 -0,009 0 -0,048 0,930 | 0,005 |
Поскольку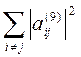 
< 0,01, расчеты прекращаем.
Ответ: l1 = -6,17; l2 = 3,65; l3 = -2,41; l4 = 0,93.
8.3 QR-алгоритм
Этот метод определения собственных значений матрицы А использует тот факт, что всякую неособенную матрицу можно представить в виде A = QR,, где Q - ортогональная матрица, а R - левая треугольная. Представление А в данном виде (QR-разложение матрицы) осуществляется при помощи итерационного процесса: строится последовательность матриц А1, А2, … , таким образом, чтобы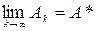 
, где А* - левая треугольная (в случае различных вещественных собственных значений), либо левая блочно-треугольная матрица, если среди собственных значений есть кратные или комплексные (см. п. 8.1). Процесс продолжают, пока не будет выполнено условие 
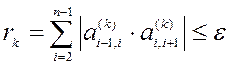. В результате на главной диагонали матрицы Ak окажутся квадратные блоки 1 – го и (или) 2 – го порядков:
 |
Блоки 1–го порядка – это собственные значения матрицы А. Чтобы найти парные собственные значения блоков 2–го порядка
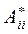, нужно решить квадратные уравнения 
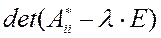= 0.
Описание QR – алгоритма.
k = 1.Будем считать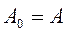 
. Умножим 
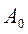на ортогональную матрицу Q1 справа, получим 
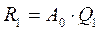. Находим 
.
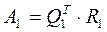k = 2. Умножаем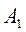 
на Q2 справа: 
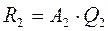, находим 
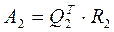и т.д.
Таким образом,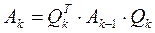 
, k = 1, 2, …,
где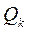 
– произведение матриц вращения:
.
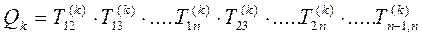Матрицы вращения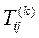 
имеют структуру, описанную в п. 4.5.1, а величины 
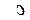и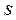 
находят по формулам:
; 
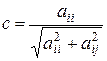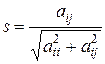с использованием элементов матрицы 
.
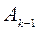В результате подобного преобразования 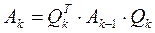матрица Ak остается симметричной, если Ak-1симметричная, или левой почти треугольной, если Ak-1– левая почти треугольная, сохраняя свои собственные значения.
Если матрица А предварительно была приведена к трехдиагональному либо левому почти треугольному виду (например, при помощи метода Гивенса), то это уменьшает количество вычислений: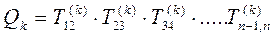 
.
Задача
Найти собственные значения матрицы А из условия задачи 2 п. 8.1. Точность 0,01.
Решение. Воспользуемся левой почти треугольной матрицей, к которой была приведена А при помощи метода Гивенса. Пусть
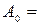
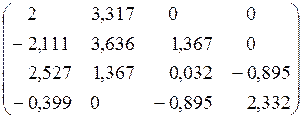
Здесь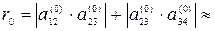 
5,757.
k = 1; A1 = QT1 × A0 × Q1 , где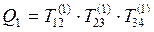 
.
Матрица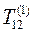 
: i = 1; j = 2; c = 0,516; s = -0,856 .
Матрица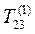 
: i = 2; j = 3; c = 0,938; s = -0,348.
Матрица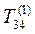 
: i = 3; j = 4; c = 0,515; s = 0,857.
; 
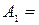
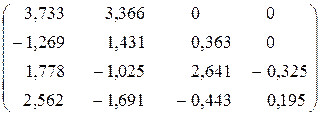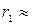1,340.
k = 2 . A2 = QT2 × A1 × Q2, где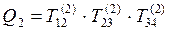 
.
Матрица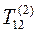 
: i = 1; j = 2; c = 0,743; s = -0,670.
Матрица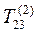 
: i = 2; j = 3; c = 0,982; s = -0,186.
Матрица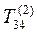 
: i = 3; j = 4; c = 0,994; s = 0,109.
; 
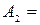
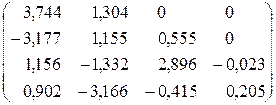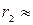0,736.
Процесс продолжаем, пока не будет выполнено условие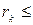 
0,01. На 58-м шагу получаем матрицу:
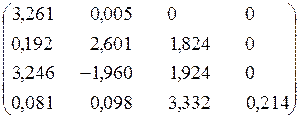
Здесь l1 = 3,26; l2 = 0,21. Чтобы найти комплексные собственные значения l3,4 , решаем уравнение
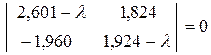. Получим l3,4 = 2,26 ± 1,86i
Ответ: l1 » 3,26; l2 » 0,21; l3,4 » 2,26 ± 1,86i
Литература
[7], гл. VI, § 1,2,3
[8], гл. VIII , § 8.4
[9], гл. VI, § 14,15
Конспект лекций.
СПИСОК ЛИТЕРАТУРЫ
1. Воробьева Г. Н., Данилова А. Н. Практикум по численным методам - М.: Высшая школа,1979.
2. Данко П.Е. Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.: Высшая школа, 1980, ч.1,2 .
3. Задачи и упражнения по математическому анализу для втузов./Под ред. Б.П.Демидовича/ - М., Наука,1970 (и послед.издания).
4. Березин И. С., Жидков Н. П. Методы вычислений - Физмагиз,1962, т.1,2.
5. Данилина Н. И., Дубровская Н.С. и др. Численные методы - М.: Высшая школа,1976.
Дата добавления: 2021-07-22; просмотров: 338;
Поиск по сайту
Узнать еще
- Andantino con moto А. Бородин. Для берегов отчизны дальней
- B — число подмножеств, то частное а : b - это число элементов в каждом подмножестве.
- I тип реакций. Реакции, характерные для органических кислот.
- I. 5. Тесты для контроля знаний раздела I
- II раздел. Организация работы логопеда в группе для детей с ОНР
- II. Стоимость отдельных элементов капитала
- III. Биогеохимические циклы элементов и веществ (на примере основных биогенных элементов: углерод, азот, фосфор) и их количественные характеристики.
- III. Здания для проживания людей
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
