Вычисление двойного интеграла
Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и j £ y, тогда
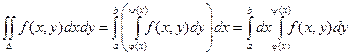



 y y = y(x)
y y = y(x)

D
y = j(x)
 a b x
a b x
Пример. Вычислить интеграл 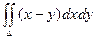 , если область D ограничена линиями: y = 0, y = x2, x = 2.
, если область D ограничена линиями: y = 0, y = x2, x = 2.
 y
y
D
0 2 x
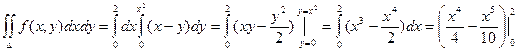 =
= 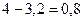
Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то
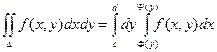
Пример. Вычислить интеграл 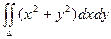 , если область D ограничена линиями
, если область D ограничена линиями
y = x, x = 0, y = 1, y = 2.
y

y = x
D
0 x
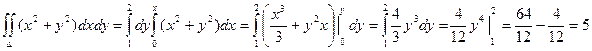
Пример. Вычислить интеграл 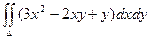 , если область интегрирования D ограничена линиями х = 0, х = у2, у = 2.
, если область интегрирования D ограничена линиями х = 0, х = у2, у = 2.
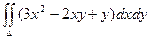 =
= 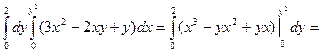
= 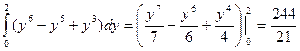
Геометрические приложения кратных интегралов
Вычисление площадей в декартовых координатах.
 y
y
y = j(x)
S
y = f(x)
a b x
Площадь S, показанная на рисунке может быть вычислена с помощью двойного интеграла по формуле:
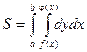
Пример. Вычислить площадь фигуры, ограниченной линиями y2 = 4x + 4; x + y – 2 = 0.
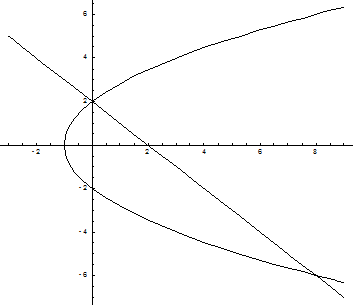
Линии пересекаются в двух точках – (0, 2) и (8, -6). Таким образом, область интегрирования ограничена по оси Ох графиками кривых от 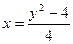 до х = 2 – у, а по оси Оу – от –6 до 2. Тогда искомая площадь равна:
до х = 2 – у, а по оси Оу – от –6 до 2. Тогда искомая площадь равна:
S = 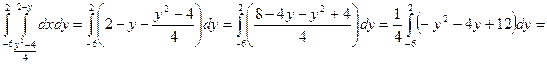
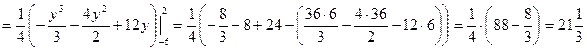
Дата добавления: 2020-06-09; просмотров: 750;











