Алгоритм построения обратной матрицы.
1) Вычислить определитель матрицы А. Если определитель равен нулю, то обратной матрицы не существует.
2) Если определитель матрицы не равен нулю, то составить из алгебраических дополнений соответствующих элементов матрицы А матрицу 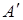 .
.
3) Транспонируя матрицу 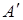 , получить присоединенную матрицу
, получить присоединенную матрицу 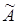 .
.
4) По формуле (2) составить обратную матрицу 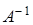 .
.
5) По формуле (1) проверить вычисления.
Пример. Найти обратную матрицу.
а). Пусть А= 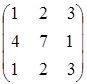 . Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
. Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
б). Пусть А= 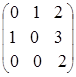 .
.
Вычислим определитель матрицы
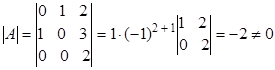
 обратная матрица существует.
обратная матрица существует.
Составим матрицу из алгебраических дополнений
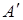 =
= 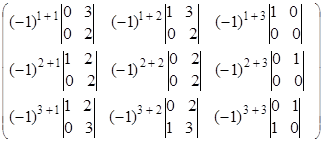 =
= 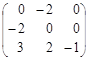 ;
;
транспонируя матрицу 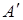 , получим присоединенную матрицу
, получим присоединенную матрицу 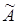

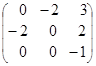 ;
;
по формуле (2) найдем обратную матрицу 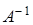
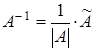 =
= 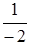
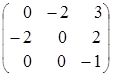 =
=  .
.
Проверим правильность вычислений

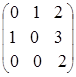
 =
=
= 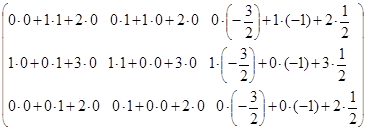 =
= 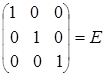 .
.
Следовательно, обратная матрица построена верна.
4. ЗАДАЧИ И УПРАЖНЕНИЯ 
4.1 Матрицы и действия над ними
1. Найти сумму, разность, произведения двух матриц А и В.
а) 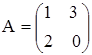 ,
, 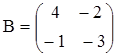 ;
;
б) 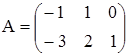 ,
, 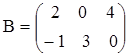 ;
;
в) 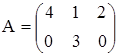 ,
, 
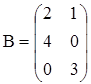 ;
;
Дата добавления: 2021-09-07; просмотров: 750;











