Приведение матрицы к трехдиагональному или почти треугольному виду при помощи метода Гивенса

1) Если А - вещественная матрица, имеющая различные вещественные собственные значения l₁, l₂, . . . ,l_n , то ее при помощи последовательности подобных преобразований можно привести (с определенной точностью) к диагональному виду

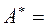
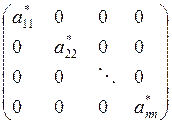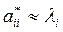, где , (i =1, 2, . . . , n).

(Столбцы результирующей матрицы U, использованной при этом, есть собственные векторы матрицы А).

2) Если среди собственных значений матрицы А есть кратные либо комплексные, то ее удается привести лишь к блочно - треугольному виду:

,

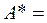
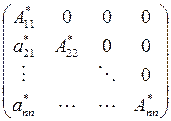где 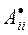- квадратные блоки 1-го и 2-го порядков, причем блоки 1-го порядка - это собственные значения матрицы А, а собственные значения блоков 2-го порядка - это пары комплексных либо кратных собственных значений матрицы А.

Процесс построения матрицы 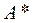- итерационный, поэтому для уменьшения числа шагов предварительно приводят А либо к трехдиагональному виду (в первом случае), либо к почти треугольному (во втором), а затем добиваются близости недиагональных элементов матрицы к нулю, насколько это возможно.

Метод Гивенса позволяет за N шагов привести матрицу А к трехдиагональному виду, если А - симметричная, либо к левому почти треугольному виду, если А - произвольная квадратная матрица. Этот процесс осуществляется посредством подобных преобразований вида:

,

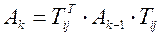где i = 2, 3, ... n - 1; j = i+1, i+2, . . . n; к = 1, 2, . . . ,N,

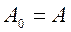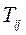; - матрица вращения.

В итоге получаем:

,

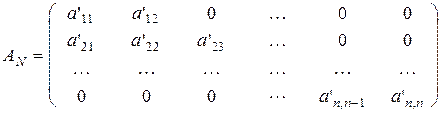если А была симметричной, либо

,

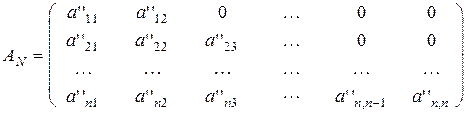если А - была произвольной матрицей.

Матрица вращения 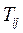имеет структуру, описанную в п.4.5.1, т.е элементы 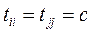; ; 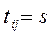, но величины 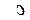и 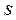вычисляют по другим формулам:

; .

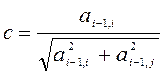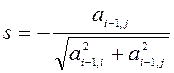В результате преобразования вида 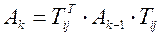обнуляется элемент 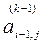матрицы 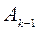, т.е. 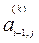= 0. Для получения матрицы 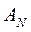потребуется 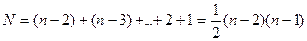таких преобразований.

Пусть T = T₂₃ × T₂₄ × . . . × T_2n × . . . × T_n-1,n, тогда

T^Т = T^T_n-1,n × . . . × T^T_2n × . . . × T^T₂₄ × T^T₂₃ и можно записать: A_N = T^T × A × T ,

где T - ортогональная матрица. Это означает, что матрица A_N подобна A и имеет те же собственные значения.

Если вместо матриц вращения использовать матрицы отражения, то аналогичный метод носит имя Хаусхолдера.

Задача 1

Дана симметричная матрица: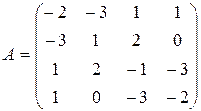

Используя метод Гивенса, привести А к трехдиагональному виду. Точность вычислений 0,01.

Решение. Для приведения матрицы А к трехдиагональному виду нужно обнулить три элемента: а₁₃, а₁₄, а₂₄. Для этого необходимо построить три матрицы вращения: Т₂₃, Т₂₄ и Т₃₄ . Будем считать 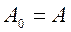. Результаты вычислений приведены в таблице.

№ шага k	i, j, c, s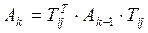
	i = 2 j = 3 c = -0,949 s = -0,316	-2 3,162 0 1 3,162 -0,4 2,2 -0,949 0 2,2 0,4 2,846 1 -0,949 2,846 -2
	i = 2 j = 4 c = 0,953 s = -0,302	-2 3,317 0 0 3,317 -1,091 2,956 -1,236 0 2,956 0,4 2,051 0 -1,236 2,051 -1,309
	i = 3 j = 4 c = 0,923 s = 0,386	-2 3,317 0 0 3,317 -1,091 3,204 0 0 3,204 -1,314 2,048 0 0 2,048 0,405

Ответ:

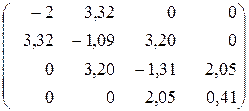
Задача 2 (для самостоятельного решения)

Дана матрица: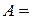

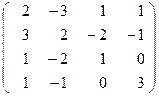
При помощи метода Гивенса привести ее к левому почти треугольному виду. Точность 0,001

Ответ: .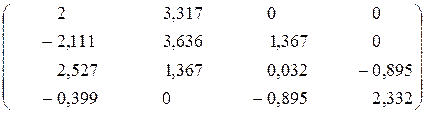

8.2 Метод Якоби и схема его реализации для получения собственных значений матрицы

Метод Якоби – итерационный метод, предназначенный для определения собственных значений симметричной матрицы А, которая при помощи цепочки подобных преобразований приводится (с определенной точностью) к матрице диагонального вида D. В процессе работы метода строится последовательность матриц , где , 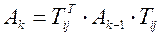, которая сходится к матрице D . Процесс считают законченным, когда

, где - элементы матрицы А_k .

(Напомним, что все собственные значения вещественной симметричной матрицы – действительные числа l₁, l₂, . . . l_n, поэтому после получения матрицы D их значения находятся на главной диагонали D).

Иногда для ускорения сходимости A_k ® D предварительно приводят матрицу А к трехдиагональному виду с использованием метода Гивенса (см. п. 8.1).

Матрицы 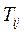, которые используются в методе Якоби – это матрицы вращения (см. п. 4.5.1), в которых элементы и вычислены по формулам

; ;

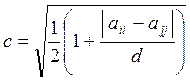Где .

При умножении 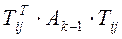обнуляются элементы a_ji и a_ij матрицы 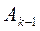, т.е. = 0. При этом матрица остается симметричной, ее собственные значения не изменяются. Однако, на каждом шаге «портятся» обнуленные на предыдущих шагах элементы матрицы, поэтому процесс приведения А к D в общем случае бесконечен.

Различные схемы реализации метода Якоби зависят от правил выбора i, j на каждом шаге. Перечислим некоторые схемы, для которых сходимость итерационного процесса доказана.