Построение обратной матрицы методом окаймления
Дана невырожденная матрица 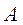 размерности
размерности 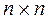 . Требуется найти обратную матрицу
. Требуется найти обратную матрицу 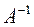 , т.е. такую матрицу, что
, т.е. такую матрицу, что 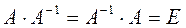 .
.
Схема метода окаймления следующая. Рассматриваем матрицы 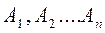 ,где
,где 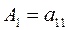 ,
, 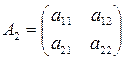 , …,
, …, 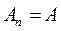 , т.е. каждая следующая матрица получается из предыдущей “окаймлением” предыдущей матрицы строкой и столбцом матрицы
, т.е. каждая следующая матрица получается из предыдущей “окаймлением” предыдущей матрицы строкой и столбцом матрицы 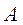 . На каждом шаге
. На каждом шаге 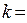 1, 2, …,
1, 2, …, 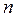 строится матрица
строится матрица 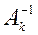 , обратная к
, обратная к 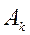 . При этом, если матрицу
. При этом, если матрицу 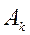 представить в форме:
представить в форме:


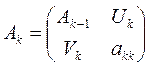 , где
, где 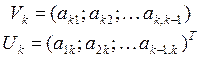 ,
,
то обратная к ней матрица 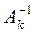 будет иметь вид:
будет иметь вид:


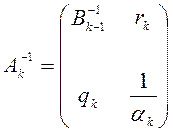 ,
,
где:
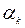 – число:
– число: 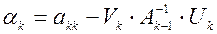 ; (1)
; (1)
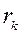 – столбец:
– столбец: 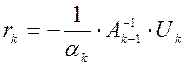 ; (2)
; (2)
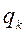 – строка:
– строка: 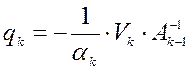 ; (3)
; (3)
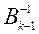 – матрица:
– матрица: 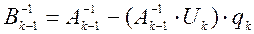 . (4).
. (4).
Таким образом, для построения 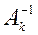 используется
используется 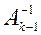 , построенная на предыдущем шаге. На
, построенная на предыдущем шаге. На 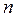 –м шаге получаем
–м шаге получаем 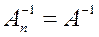 .
.
Для упрощения расчетов при 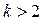 следует повторяющиеся элементы:
следует повторяющиеся элементы: 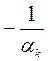 ,
, 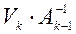 и
и 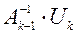 вычислять отдельно.
вычислять отдельно.
Особенно удобен метод окаймления в случае, когда требуется найти 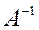 , а матрица
, а матрица 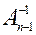 известна (здесь
известна (здесь 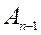 – матрица
– матрица 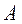 без последней строки и последнего столбца). В этом случае обращение матрицы осуществляется в 1 шаг. Можно рекомендовать этот метод для матриц
без последней строки и последнего столбца). В этом случае обращение матрицы осуществляется в 1 шаг. Можно рекомендовать этот метод для матриц 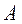 большой размерности.
большой размерности.
Задача
Получить матрицу, обратную матрице 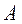 , при помощи метода окаймления. Выполнить проверку. Точность вычислений
, при помощи метода окаймления. Выполнить проверку. Точность вычислений 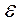 = 0,01.
= 0,01.
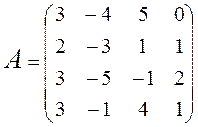 .
.
Решение.
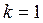 .
. 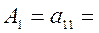 3;
3; 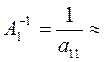 0,333.
0,333.
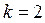 .
. 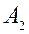
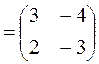 ; здесь
; здесь 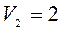 ;
; 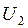 = - 4;
= - 4; 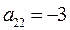 .
.
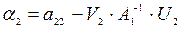
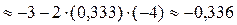 ;
; 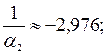
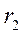
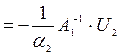
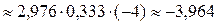 ;
;
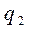
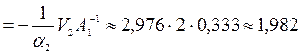 ;
;
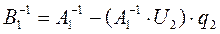
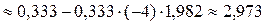 .
.
Получаем: 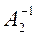
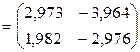 .
.
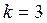 .
. 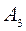
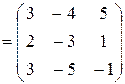 ; здесь
; здесь 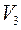
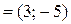 ;
; 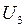
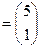 ;
; 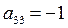 .
.
Сначала вычислим произведения
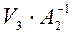
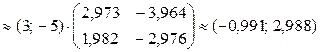 ;
;
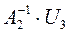
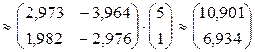 .
.
Теперь найдем 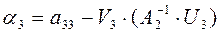
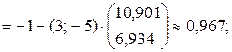
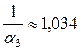 ;
; 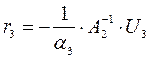
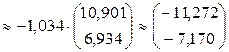 ;
;
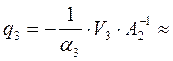
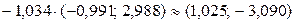 ;
;
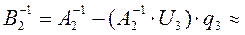
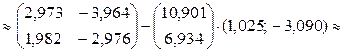
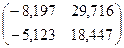 .
.
Получаем 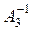
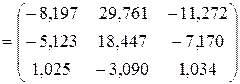 .
.
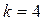 .
. 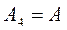 ;
; 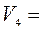 (3; –1; 4);
(3; –1; 4); 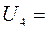 (0; 1; 2)T;
(0; 1; 2)T; 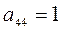 .
.
Вычисляем произведения:
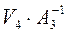
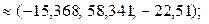
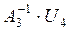
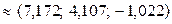 T.
T.
Теперь находим
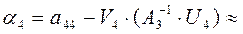 -12,321;
-12,321; 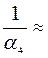 -0,081;
-0,081;
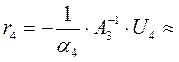 (0,581; 0,333; –0,083)T;
(0,581; 0,333; –0,083)T;
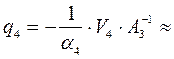 (–1,245; 4,726; –1,823);
(–1,245; 4,726; –1,823);
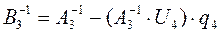
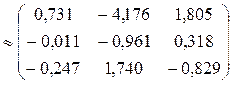 .
.
Получаем обратную матрицу
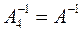
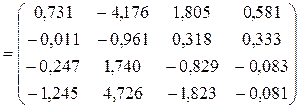 .
.
Проверки.
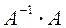
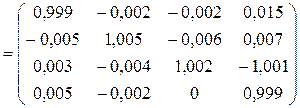 ;
;
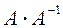
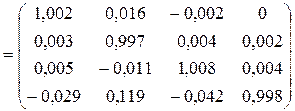 .
.
Вывод: 
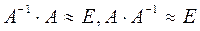 , обратная матрица построена верно.
, обратная матрица построена верно.
Ответ: 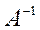
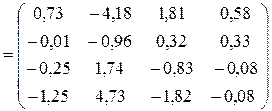 .
.
Дата добавления: 2021-07-22; просмотров: 895;











