Решение проблемы собственных значений

Напомним некоторые сведения. Если А - квадратная матрица размерности n и матричное равенство

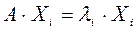
выполнено при некотором 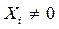, тогда l_i называют собственным значением (собственным числом) матрицы А, а ненулевой вектор X_i , соответствующий l_i , называют собственным вектором матрицы А:

.

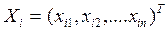Задачу получения всех собственных значений матрицы А называют полной проблемой собственных значений, в отличие от частичных проблем: определения максимального или минимального по модулю собственного значения, нахождения собственного значения, ближайшего к данному числу а и др.

Как известно, легко находятся собственные значения для треугольной и диагональной матрицы: они равны диагональным элементам данных матриц. Поэтому некоторые методы решения полной проблемы собственных значений основаны на приведении матрицы А к одному из этих видов при помощи подобных преобразований 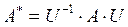. (Подобными преобразованиями матрицы А называют такие преобразования вида 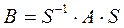, где S - невырожденная матрица, что собственные значения матриц А и В одинаковые, то есть подобные преобразования не изменяют собственных значений матрицы). В случае, когда U - ортогональная матрица, выполнено 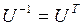и преобразование подобия можно записать так: .

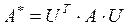После определения собственных значений матрицы А собственные векторы легко найти, решая систему однородных уравнений AX_i = l_i×X_i для каждого l_i (i =1, 2, . . . , n).