Оптимальные решения.

Вектор X* = {х₁, х₂,... х_п }^T, удовлетворяющий соотношениям (10) - (11), называется оптимальной точкой, а соответствующее значение f(X*) - оптимальным значением целевой функции. Пара X* и f(X*) составляет оптимальное решение. Как показано на примере мультимодальной (многоэкстремальной) функции на рис. 6, могут существовать различные типы оптимальных решений, если целевая функция не является унимодальной (т. е. имеющей один экстремум). Глобальное оптимальное решение представляет собой наименьшее значение f(X), тогда как локальное (или относительное) оптимальное решение представляет собой наименьшее значение f(X) в окрестности некоторого вектора X. Как для глобального, так и для локального минимума

f(X*) ≤ f(X),

но для глобального оптимального решения это соотношение выполняется для всех X в эвклидовом пространстве Е^п, тогда как для локального оптимального решения это имеет место только для малой области ξ, где норма || X - X* || < ξ. Если принимается во внимание и точность решения, то условие оптимальности можно представить в виде

f(X*) ≤ f(X) – γ,

где γ — некоторая малая величина.

Все алгоритмы, описываемые в пособии [3], дают лишь локально оптимальные решения, так как на каждом этапе решения при движении к точке экстремума X* они зависят в основном от локальных свойств (местной топографии) целевой функции и ограничений. Работа всех поисковых алгоритмов примерно одинакова: на основании исследования топографии целевой функции в текущей точке определяется характер её изменения и в пространстве проектных переменных делается рабочий шаг в направлении её уменьшения (или увеличения). Далее, процесс повторяется. Исключение составляют чистые методы Монте-Карло, которые исследуемые точки выбирают случайным образом. Однако эти методы вообще не гарантируют ничего: экстремум они находят случайно, если вообще находят.

На практике предположение о том, что локальный экстремум является глобальным, может быть проверено путем использования нескольких начальных векторов, но даже если найдено только одно локальное решение, в общем случае нельзя показать, что это решение обязательно является глобальным оптимумом.

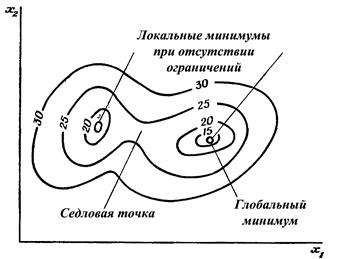
Рис. 6. Классификация оптимальных решений.

К счастью, для задач, соответствующих действительным физическим процессам, целевая функция обычно является хорошей и обладает единственным экстремумом. Поэтому для большинства практических целей использование численных процедур, дающих локальное решение задачи оптимизации, не является большим недостатком.