Задача линейного программирования.

Задачей линейного программирования называется задача, в которой минимизируемым или максимизируемым критерием является линейная функция, причем на переменные налагаются ограничения, которые также представляются линейными функциями. Комбинация скаляров или векторов, обычно обозначаемых X_i,называется линейной, если она может быть записана в виде

с₁Х₁ + с₂Х₂+ ... +с_n Х_n , (1)

где все коэффициенты с — константы. Например, функция

4 х₁+ 3 х₂+ 5 x₃ + 2

линейна относительно переменных x₁ , x₂ , x₃ , тогда как функция

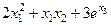
не линейна относительно тех же переменных. Величины Х₁..., Х_nназываются линейно зависимыми, если для некоторого набора c_i в предположении, что не все c_i равны нулю, имеет место следующее равенство:

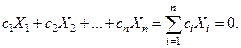(2)

С другой стороны, если 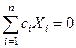только тогда, когда все коэффициенты с_i равны нулю, то величины Х_i ... Х_п называются линейно независимыми.

Линейное программирование стало быстро развиваться после второй мировой войны, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности. Применение линейного программирования оказалось плодотворным в таких областях, как:

1. Оптимальное регулирование полетов на воздушных линиях.

2. Распределение во времени транспортировки грузов с заводов и складов к базам.

4. Планирование промышленного производства.

5. Система оплаты контрактов.

6. Проектирование систем связи и распределение в них потоков сообщений.

7. Распределение кадров.

8. Организация максимальных потоков в транспортных сетях.

Широкое привлечение внимания к линейному программированию привело к тому, что до некоторой степени была преувеличена его значимость; часто упускали из виду, что оно применимо лишь тогда, когда выполняются лежащие в его основе допущения, которые в свою очередь базируются на линейном математическом представлении реального мира. В нелинейном программировании не используются столь сильные упрощения.

Хотя задача линейного программирования может быть сформулирована по-разному, запишем ее в следующей форме:

минимизировать 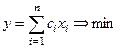(3)

при ограничениях

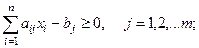(4)

(5)

где a, b и с — константы, а х_i — искомые переменные.

Уравнения (3)-(5) можно компактно записать в матричной форме. Пусть X и с – вектор-столбцы размерности (n ´ 1); а–матрица констант размерности (n ´ m) и b– вектор-столбец размерности (m ´ 1):

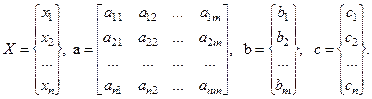
Тогда в матричных обозначениях уравнения (3)-(5) запишутся следующим образом:

минимизировать 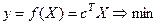(6)

при ограничениях

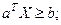(7)

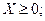(8)

где верхний индекс Т означает транспонирование.

Для решения задачи, выраженной уравнениями (6)-(8), были предложены различные методы, один из которых (симплекс-метод) стал общеупотребительным и который, в частности, кратко рассмотрен в учебном пособии по методам оптимизации [3].

Пример. Этот пример иллюстрирует связь между уравнениями (3)-(5) и реальной задачей. Крупная авиакомпания ассигновала 600 млн. долл. на лизинг самолётов трех типов. Годовой лизинг самолёта А стоит 10 млн. долл., самолёта В — 20 млн. долл. и самолёта С — 23 млн. долл. Сколько самолётов каждого типа нужно заказать, чтобы получить наибольшую производительность в тонно-километрах на один день с учетом приведенных ниже условий?

Самолёт А требует для эксплуатации одного экипажа на каждую смену, максимальное число смен в сутки 3, производительность 21000 тонно-километров за каждую смену.

Самолёт В требует двух экипажей на каждую смену, максимальное число смен в сутки 3, производительность 36000 тонно-километров за каждую смену.

Самолёт С требует двух экипажей на каждую смену, максимальное число смен в сутки 3, производительность 37800 тонно-километров за каждую смену.

Кроме того, число экипажей должно быть не больше 145, число самолётов — не больше 30.

Эта задача может быть сформулирована в терминах линейного программирования следующим образом. Обозначим число смен индексами 1, 2 и 3, а число самолётов каждого типа — прописными буквами А, В и С. Таким образом А₁ означает количество самолётов типа А, работающих одну смену в сутки.

Сначала необходимо выбрать функцию цели. В данном примере критерием оптимальности является производительность, соответствующая функции (3):

у = 21000А₁ + 42000А₂ + 63000А₃ + 36000В₁ + 72000В₂ + 108000В₃ + 37800С₁ + 75600С₂ + 113400С₃,

где у - количество тонно-километров. Запишем далее выражения для ограничений. Здесь мы имеем дело с ограничениями трех типов: 1) общая стоимость лизинга всех самолётов не должна превышать 600 млн. долл.; 2) количество самолётов должно быть не более 30; 3) количество экипажей должно быть не более 145:

1) 10 млн. (А₁ + А₂ + А₃) + 20 млн.(В₁ + В₂ + В₃) + 23 млн. (С₁ + С₂ + С₃)≤ 600 млн.;

2) А₁ + A₂ + A₂ + B₁ + B₂ + B₃ + C_l + C₂ + С₃ ≤ 30;

3) А₁ + 2А₂ + 3А₃ + 2В₁ + 4B₂ + 6В₃ + 2С₁ + 4С₂ + 6С₃ ≤ 145.

Кроме того, поскольку самолёты являются физическими объектами, то их количество не может быть отрицательной величиной, и тогда имеют место следующие неравенства, соответствующие условиям (5):

A_i ³ 0, B_i ³ 0, C_i ³ 0, i = 1, 2, 3.

Поставленная таким образом задача может быть решена соответствующим методом линейного программирования; в результате определяется количество самолётов типов А, В и С, максимизирующее величину целевой функции (производительность) у.

Решение: 12 самолётов типа А, 0 самолётов типа В и 18 самолётов типа С.