Задачи для самостоятельного решения.
1. Решить задачу Коши 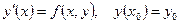 на отрезке [x0, X] методом Рунге-Кутта четвертого порядка, применяя деление отрезка на N частей. Оценить погрешность.
на отрезке [x0, X] методом Рунге-Кутта четвертого порядка, применяя деление отрезка на N частей. Оценить погрешность.
| № вари -анта | Дифференциальное уравнение | Начальное условие | [x0, X] | N |
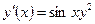
| y(0) = 1 | [0, 2] | ||
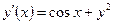
| y(0) = 2 | [0, 2] | ||
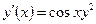
| y(0) = 3 | [0, 2] | ||
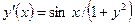
| y(0) = 1 | [0, 2] | ||
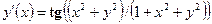
| y(0) = 2 | [0, 2] | ||
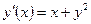
| y(1) = 3 | [1, 2] | ||
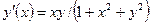
| y(1) = 1 | [1, 2] | ||
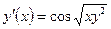
| y(1) = 2 | [1, 2] | ||
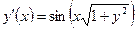
| y(1) = 3 | [1, 2] | ||
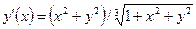
| y(1) = 1 | [1, 2] | ||
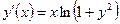
| y(1) = 2 | [1, 3] | ||
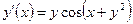
| y(1) = 3 | [1, 3] | ||
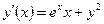
| y(1) = 1 | [1, 3] | ||
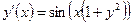
| y(1) = 2 | [1, 3] | ||
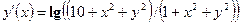
| y(1) = 3 | [1, 3] | ||
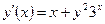
| y(–1) = 1 | [–1, 1] | ||
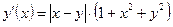
| y(–1) = 2 | [–1, 1] | ||
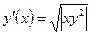
| y(–1) = 3 | [–1, 1] | ||
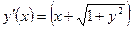
| y(–1) = 1 | [–1, 1] | ||
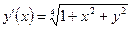
| y(–1) = 2 | [–1, 1] | ||
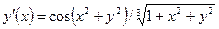
| y(0) = 3 | [0, π] | ||
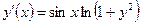
| y(0) = 1 | [0, π] | ||
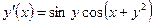
| y(0) = 2 | [0, π] | ||
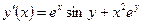
| y(0) = 3 | [0, π] | ||
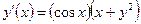
| y(0) = 1 | [0, π] | ||
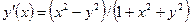
| y(π/2) = 2 | [π/2, π] | ||
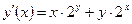
| y(π/2) = 3 | [π/2, π] | ||
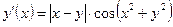
| y(π/2) = 1 | [π/2, π] | ||
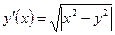
| y(π/2) = 2 | [π/2, π] | ||
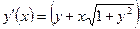
| y(π/2) = 3 | [π/2, π] |
2. Решить задачу Коши для дифференциального уравнения сведением к задаче Коши для системы уравнений первого порядка.
| № вари -анта | Дифференциальное уравнение | Начальные условия | [x0, X] | N |
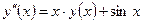
| y(0) = 1, 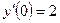
| [0, 2] | ||
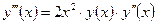
| y(0) = 2, 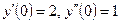
| [0, 2] | ||
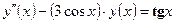
| y(0) = 3, 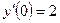
| [0, 2] | ||
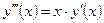
| y(0) = 1, 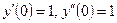
| [0, 2] | ||
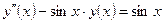
| y(0) = 2, 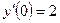
| [0, 2] | ||
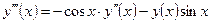
| y(1) = 3, 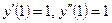
| [1, 2] | ||
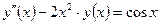
| y(1) = 1, 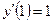
| [1, 2] | ||
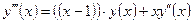
| y(1) = 2, 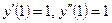
| [1, 2] | ||
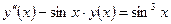
| y(1) = 3, 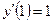
| [1, 2] | ||
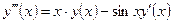
| y(1) = 1, 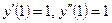
| [1, 2] | ||
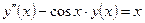
| y(1) = 2, 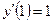
| [1, 3] | ||
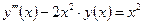
| y(1) = 3, 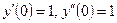
| [1, 3] | ||
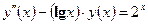
| y(1) = 1, 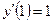
| [1, 3] | ||
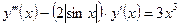
| y(1) = 2, 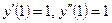
| [1, 3] | ||
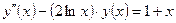
| y(1) = 3, 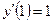
| [1, 3] | ||
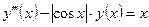
| y(–1) = 1, 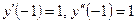
| [–1, 1] | ||
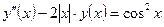
| y(–1) = 2, 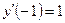
| [–1, 1] | ||
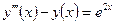
| y(–1) = 3, 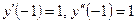
| [–1, 1] | ||
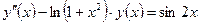
| y(–1) = 1, 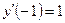
| [–1, 1] | ||
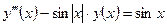
| y(–1) = 2, 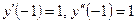
| [–1, 1] | ||
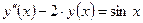
| y(0) = 3, 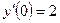
| [0, π] | ||
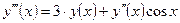
| y(0) = 1, 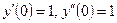
| [0, π] | ||
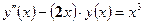
| y(0) = 2, 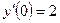
| [0, π] | ||
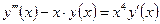
| y(0) = 3, 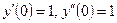
| [0, π] | ||
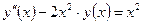
| y(0) = 1, 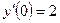
| [0, π] | ||
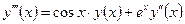
| y(2) = 2, 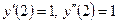
| [2, π] | ||
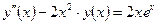
| y(2) = 3, 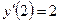
| [2, π] | ||
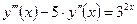
| y(2) = 1, 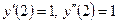
| [2, π] | ||
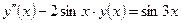
| y(2) = 2, 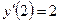
| [2, π] | ||
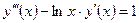
| y(2) = 3, 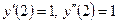
| [2, π] |
3. Написать формулы метода прогонки для решения краевой задачи:
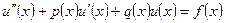
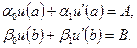
4. Написать формулы метода пристрелки для решения краевой задачи
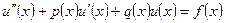
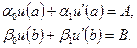
Дата добавления: 2021-09-07; просмотров: 398;











