Нахождение исходного допустимого базисного решения.
Как и в других ЗЛП, итерационный процесс отыскания оптимального плана ТЗ начинается с какого-либо исходного допустимого базисного решения. Опорный план строим в виде матрицы размером m*n. Заполненные позиции матрицы, то есть такие, в которых 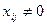 , соответствуют базисным неизвестным. Заносим эти значения в соответствующую клетку таблицы перевозок в правый нижний угол. Отметим, что математическая модель Т3 (22) – (25) обладает следующими особенностями: система ограничений (23), (24) является совместной, неопределённой и следовательно, имеет бесчисленное множество решений; число линейно-независимых уравнений системы всегда на одно меньше общего количества уравнений в системе. Следовательно, ранг матрицы системы уравнений не более m+n-1; элементами матрицы системы (23), (24) являются только единицы и нули.
, соответствуют базисным неизвестным. Заносим эти значения в соответствующую клетку таблицы перевозок в правый нижний угол. Отметим, что математическая модель Т3 (22) – (25) обладает следующими особенностями: система ограничений (23), (24) является совместной, неопределённой и следовательно, имеет бесчисленное множество решений; число линейно-независимых уравнений системы всегда на одно меньше общего количества уравнений в системе. Следовательно, ранг матрицы системы уравнений не более m+n-1; элементами матрицы системы (23), (24) являются только единицы и нули.
Таким образом опорный план ТЗ может иметь не более m+n-1 отличных от нуля неизвестных. Если в опорном плане число отличных от нуля компонент равно m+n-1, то план считается невырожденным, а если меньше, то вырожденным. Считаем, для определённости, что на каждом этапе решения транспортной задачи число базисных переменных ровно m+n-1, причём в случае вырожденного решения какие-то переменные xij = 0 полагаем базисными переменными.
Метод северо-западного угла (СЗУ) или диагональный метод.
Заполнение таблицы перевозок начинается с левого верхнего (северо-западного) угла. На каждом шаге заполнения стараемся наиболее полно удовлетворить потребность в грузе за счёт имеющихся запасов, продвигаясь по таблице вниз по столбцу или вправо по строке, т.е. по диагонали.
Пример. Найти первоначальное базисное распределение поставок для ТЗ, заданной таблицей 4:
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | B4 | запасы |
| A1 | 5 | 2 | 5 | 6 | ||
| A2 | 3 | 1 | 3 | 7 | ||
| A3 | 4 | 5 | 4 | 6 | ||
| потребности |
Таблица 4
Решение. Дадим переменной x1 1 максимально возможное значение, что тоже максимально возможную поставку в клетку (1,1) таблицы поставок: x1 1=min (60,40)=40. Таким образом, спрос первого потребителя полностью удовлетворён, а поэтому первый столбец таблицы выпадает из последующего рассмотрения. Заполненную клетку штрихуем. В оставшейся таблице опять находим северо-западный угол. В нашем случае это клетка (1,2) и дадим туда максимально возможную поставку, учитывая, что первый поставщик уже отдал 40 едениц груза, то есть x1 2 = min(60-40,80)=20. После этого мощность первого поставщика полностью реализована, и из рассмотрения выпадает первая строка таблицы поставок. В оставшейся таблице снова находим северо-западный угол и т.д. Построенное исходное допустимое базисное решение представлено в таблице 5.
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | B4 | запасы |
| A1 | 5 40 | 2 20 | 5 | 6 | ||
| A2 | 3 | 1 80 | 3 20 | 7 | ||
| A3 | 4 | 5 | 4 30 | 6 40 | ||
| потребности |
Таблица 5
Ответ:
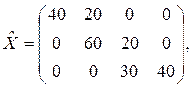
f0=5*40+2*20+1*60+3*20+4*30+6*40=720.
Число заполненных клеток оказалось равным 6, т.е. числу базисных переменных m+n-1.
Метод северо-западного угла имеет существенный недостаток: он построен без учёта коэффициентов затрат задачи, и поэтому, как правило, построенное этим методом решение «дальше» от оптимального, чем построенное методом наименьшей сложности.
Дата добавления: 2020-02-05; просмотров: 789;











