Метод множителей Лагранжа.

Этот метод широко используется при оптимизации авиационных агрегатов при их проектировании с учётом многообразных и разнородных ограничений, например: проектирование конструкции с учётом ограничений по прочности, жёсткости, частотам собственных колебаний, устойчивости и т.п. Поэтому краткое знакомство на уровне идей с методом множителей Лагранжа представляется полезным.

Методы, основанные на использовании множителей Лагранжа, относятся к категории параметрических методов штрафных функций, поскольку для них характерно то, что функции-ограничения вводятся в структуру модифицированной целевой функции совместно с некоторым переменным параметром. Чтобы обобщить метод множителей Лагранжа, ограничения в виде неравенств следует преобразовать в ограничения, имеющие вид равенств, путём введения надлежащих ослабляющих переменных (на каждое ограничение-неравенство по одной ослабляющей переменной). Задача нелинейного программирования в общей постановке принимает при этом следующий вид:

минимизировать f(X), X Î Еⁿ ; (29)

при ограничениях

h_j (X) = 0; j = 1,2 ... m; (30)

g_j (X) – v_j² = 0; j = (т + 1) ... р. (31)

Если вычесть v_j² из g_j (X) (j = т + 1, ... р), то можно гаранти­ровать, что ограничивающее условие, имеющее в исходной постановке задачи вид неравенства, действительно выполняется. Тогда можно определить обычным образом функцию Лагранжа

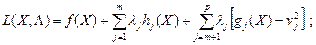(32)

где 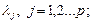- неотрицательные и не зависящие от X весовые коэффициенты, которые можно отождествить с множителями Лагранжа. Для того чтобы X* было решением общей задачи нелинейного программирования (29)-(31), необходимо и достаточно, чтобы: 1) функция f(X*) была выпуклой; 2) в окрестности X* ограничения задачи были выпуклы и 3) в точке X* удовлетворялась следующая система уравнений, определяющая стационарное решение уравнения (32):

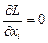; при i = 1, 2...п;

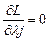; при j = l, 2 … р;

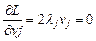; при j = (m+1)…p;

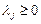; j = 1,2…p.

Короче говоря, условный минимум f(X) имеет место в стационарной точке для L(X, Λ, V) и, в частности, в седловой точке (X, Λ, V) - пространства, так что задача с ограничениями превращается в задачу определения седловой точки в отсутствие ограничений.

Заключение.

На этом мы завершаем краткое рассмотрение общей теории оптимизации. Конечно, мы не исчерпали весь круг проблем, необходимых для решения при оптимизации, однако теперь читатель сможет уверенно и компетентно формулировать задачи оптимизации организационных и технических систем, классифицировать их и выбирать для их решения наиболее эффективные поисковые алгоритмы, большой набор которых приведен в книге [4].

За рамками пособия осталась большая область теории, связанной с многопараметрической оптимизацией, с инженерными методами оптимизации, а также с оптимизацией в условиях неопределённости. Поэтому данная тонкая книжка должна рассматриваться как введение в большой и плодотворный мир оптимального проектирования организационно-технических систем.

Литература

1. Уайлд Д. Оптимальное проектирование. -М: Мир, 1981. -272с.
2. Батищев Д.И. Методы оптимального проектирования. М.: Радио и связь, 1984
3. Данилин А.И. Методы оптимизации. Учебное пособие. –Самара: Изд-во Самарского государственного аэрокосмического ун-та, 2011. -66c.
4. Химмельблау Д. Прикладное нелинейное программирование. М: Мир, 1975. -534с.