Сведение задачи с ограничениями к безусловно экстремальной форме.

Поисковые методы отыскания экстремума в задачах с явным учётом ограничений являются инструментом очень тонким и расточительным в смысле вычислительных ресурсов. С другой стороны, методы, разработанные для безусловной оптимизации, обладают высоким быстродействием, требуют относительно небольшой памяти и позволяют решать практические задачи в автоматическом режиме без каких-либо настроек алгоритмов [3].

В этой связи заманчиво преобразовать исходную задачу с ограничениями в эквивалентную задачу без ограничений, причём такое преобразование должно обеспечивать совпадение точек экстремума исходной и преобразованной задачи. Основным методом сведения задачи условной оптимизации к безусловно экстремальной форме является метод штрафных функций.

Идея метода проста: если мы ищем минимум целевой функции и, если текущая точка поиска находится внутри допустимой области, то штрафная добавка к значению целевой функции не прибавляется; если же какое-либо ограничение нарушено, то к целевой функции прибавляется штрафная добавка, пропорциональная степени нарушения ограничения. В случае поиска максимума штрафная добавка должна вычитаться.

Это заставляет поисковый алгоритм работать внутри допустимой области и при попытке выхода из неё, возвращаться обратно.

Методы штрафных функций существуют в различных вариантах, которые, отличаются способом формирования штрафной добавки, однако, имеют одну общую черту: во всех этих методах осуществляется преобразование задачи нелинейного программирования при наличии ограничений либо в одну (эквивалентную исходной) задачу без ограничений, либо в эквивалентную последовательность задач без ограничений. Пусть, например, мы хотим найти минимум функции

f(X) = (x₁ - 3)² + (х₂ - 2)²

при ограничении

h(X) = х₁ + х₂ - 4 = 0.

Прибавим h²(X) к целевой функции f(X), в результате чего получим новую целевую функцию

Р(X) = (x₁ - 3)² + (х₂ - 2)² + (х₁ + х₂ - 4)²,

значения которой будем считать свободными от каких-либо ограничений (h²(X) здесь выступает в роли «штрафа»). В процессе минимизации Р(X) «штрафная добавка» к f(X) способствует тому, чтобы вектор X в некоторой степени удовлетворял исходному ограничивающему условию h(X) = 0. Совершенно очевидно, что, пока условие h(X) = 0 удовлетворяется (в пределах установленного допуска), значение штрафного члена пренебрежимо мало, и Р(X*) → f(X*) при X → X*. Преимущество, которое мы получаем за счет перехода от задачи минимизации при наличии ограничений к задаче минимизации в отсутствие ограничений, состоит в том, что в последнем случае минимизация может осуществляться с помощью гораздо более простых (по сравнению с первым случаем) алгоритмов. При использовании методов штрафных функций получается максимальный оптимизирующий эффект за счет постоянного компромисса между необходимостью удовлетворения ограничений и процессом минимизации f(X), который достигается путем присвоения надлежащих весов целевой функции и функциям, задающим ограничения.

На рис. 13 графически представлена преобразованная целевая функция, полученная путем добавления к f(X) штрафной функции (с весовым коэффициентом, равным единице). Отметим, что точка минимума X* у обеих функций одинакова.

Методы штрафных функций можно разделить на два класса: 1) параметрические и 2) непараметрические методы.

Непараметрические методы рассматривают целевую функцию как функцию, задающую дополнительное искусственное ограничение, постепенно «уплотняемое» по мере получения информации в ходе поиска. Непараметрические методы, на наш взгляд, это просто игра ума специалистов по вычислительной математике, результаты которой иногда, к их удивлению, позволяет решить какую-то практическую задачу.

Нам нужны надёжные автоматические методы, поэтому мы рассмотрим только параметрические методы штрафных функций. Название этих методов говорит о том, что в структуру штрафной функции, которая строится с помощью функций-ограничений, входят подобранные параметры в качестве весовых коэффициентов.

Параметрические методы распадаются на три категории: 1) методы внутреннего штрафа; 2) методы внешнего штрафа и 3) комбинированные методы.

При использовании методов внутреннего штрафа значение целевой функции удерживается в отдалении от границы допустимой области, то есть точка X^(k) постоянно находится внутри допустимой области с помощью штрафной функции. Методы внешней точки, наоборот, генерируют последовательность точек, которые выходят за пределы допустимой области, но дают в пределе допустимое решение. Штрафная функция не позволяет вектору X слишком удаляться от границы допустимой области. В комбинированных методах, использование которых особенно необходимо в случае, когда явно учитываются ограничения в виде

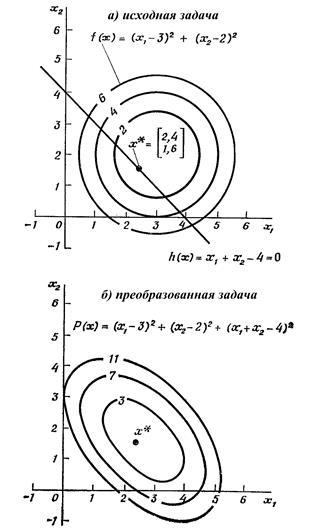
Рис. 13. Линии уровней исходной а) и преобразованной б) задачи.

равенств, в ходе минимизации одни из ограничивающих условий удовлетворяются, а другие не удовлетворяются; однако все условия в пределах заданного допуска оказываются удовлетворенными при достижении оптимального решения.

Формулировка большинства технических задач содержит только ограничения-неравенства; в организационно-экономических задачах часто имеют место ограничения-равенства, например, нужно оптимальным образом потратить определённый ресурс, - однако равенства легко преобразуются в ограничения-неравенства путем задания небольшого допуска:

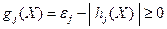, (23)

где 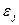- величина допуска нарушения ограничения 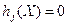. С учетом этого, будем считать, что имеем дело только с ограничениями-неравенствами, то есть формулировку задачи нелинейного программирования (9), (10), (11) сокращаем, модифицируем и применяем в виде, характерным для технических задач:

минимизировать 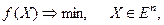(24)

при р линейных и (или) нелинейных ограничениях в виде неравенств

(25)