Задачи для самостоятельного решения.
1). Доказать с помощью законов алгебры множеств следующие тождества:
а) 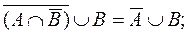
б) 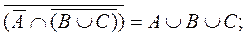
в) 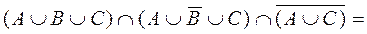 Æ.
Æ.
2) Доказать, что из 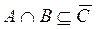 и
и 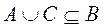 следует
следует 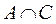 =Æ
=Æ
3) Доказать следующие соотношения для мощностей конечных множеств:
а) 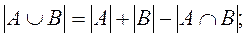
б) 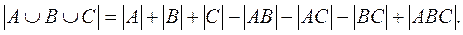
4) Доказать счётность множества рациональных чисел, указав способ их перечисления.
5). Установить взаимно однозначное соответствие между заданными множествами, указав соответствующую биекцию:
а) [0;1] и [0;2];
б) (-1;1) и (-∞; ∞).
6). Отношение R на множестве Z определяется следующим образом:
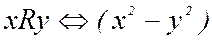 делится на 3.
делится на 3.
Показать что R есть отношение эквивалентности, найти число классов эквивалентности и описать их.
7). На системе множеств {a},{a,b},{b,c},{a,c},{a,b,c} с частичным порядком по включению указать минимальные, максимальные, наименьший и наибольший элементы.
8).Показать, что отношение “х делит y” является отношением частичного порядка на множестве N.
9). Построить таблицу умножения в кольце классов вылетов:
а) по модулю 5;
б) по модулю 6.
В чём принципиальное различие колец а) и б) ?
10). Булева функция от трёх переменных задана таблицей:
| x1 x2 x3 | F(x1 x2 x3) |
| 0 0 0 | |
| 0 0 1 | |
| 0 1 0 | |
| 0 1 1 | |
| 1 0 0 | |
| 1 0 1 | |
| 1 1 0 | |
| 1 1 1 |
Показать, что данная функция имеет две минимальные д. н. ф., Найдя их с помощью операций булевой алгебры и дав геометрическую интерпретацию на единичном кубе.
11).Построить таблицу истинности для высказывания:
а) (P ® (Q ® R)) ® ((P ® Q) ® (P ® R));
б) (P Ù (Q Ú 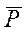 )) Ù ((
)) Ù (( 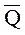 ® P) Ú Q) .
® P) Ú Q) .
12).Число А называется пределом функции y = f (x) при x ® a, если для любого сколь угодно малого ε > 0 существует δ > 0 такое, что при выполнении неравенства 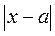 < δ выполняется неравенство
< δ выполняется неравенство
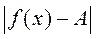 <ε.
<ε.
Запишите это определение на языке предикатов и кванторов.
13). Проверить правильность следующего рассуждения. Если Джонс не встречал этой ночью Смита, то либо Смит был убийцей, либо Джонс лжёт.
Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. Если убийство было совершено после полуночи, то либо Смит был убийцей, либо Джонс лжёт. Следовательно, Смит был убийцей.
14). «Вернувшись домой, Мегрэ позвонил на набережную Орфевр.
- Говорит Мегрэ. Есть новости ?
- Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжёт. Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи. Инспектор Люка просил передать Валг, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет.
- Немедленно задержите Этьена.»
Логически обоснуйте действия комиссара Мегрэ, принимая во внимание наряду с полученной от инспекторов информацией также известный Мегрэ факт, что трезвый Франсуа никогда не лжет.
15). Среди n монет имеется одна фальшивая вес которой меньше. Результатом взвешивания является определение, что на одной из чашек весов находится больший или меньший вес, или веса одинаковы. Указать алгоритм, гарантирующий нахождения фальшивой монеты за не более ]log3 n[ взвешиваний.
16). Выяснить, применима ли машина Тьюринга, задаваемая программой
q1 1 q2 1 R
q1 1 q1 0 R
q2 0 q3 1 R
q2 1 q3 0 L
q3 0 q1 0 R
q3 1 q0 1 C,
к слову Р.
а) Р=1031
б) Р=[10]21.
17). Построить в алфавите {0,1} машину Тьюринга, которая применима к словам вида 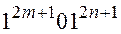
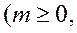
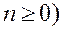 и
и 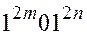
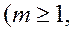
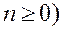 , но не применима к словам вида 12m012n-1 и 12n-1012m
, но не применима к словам вида 12m012n-1 и 12n-1012m 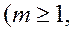
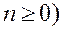 . К словам иного вида машина может быть как применима, так и не применима.
. К словам иного вида машина может быть как применима, так и не применима.
Итоговый тест.
1. Даны множества 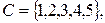
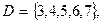 и
и 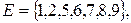 результатом операций
результатом операций 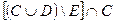 является множество: а)
является множество: а) 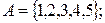 б)
б) 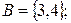 в)
в) 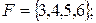 г)
г) 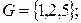
2. Даны множества 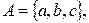
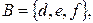 Декартовым произведением
Декартовым произведением 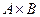 является множество: а)
является множество: а) 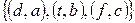 б)
б) 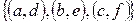 в)
в) 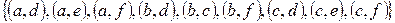 г)
г) 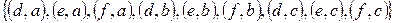
3. На множестве 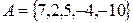 задано бинарное отношение
задано бинарное отношение 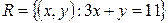 какая из пар не принадлежит R? а)
какая из пар не принадлежит R? а) 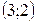 ; б)
; б) 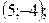 в)
в) 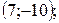 г)
г) 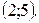
4. Если функция является сюръекцией будет ли она инъекцией а) да; б) нет; в) не обязательно.
5. Выражение 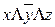 называют: а) элементарной конъюнкцией, б)элементарной дизъюнкцией
называют: а) элементарной конъюнкцией, б)элементарной дизъюнкцией
6. Упростить 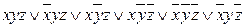 а)
а) 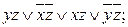 б)
б) 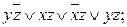 в)
в) 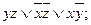 г)
г) 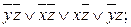
7. Квантор существования обозначают: а)"; б)$; в)!; г)~.
8. Значком “=>” обозначают; а) конъюнкцию; б) дизъюнкцию; в) импликацию; г) эквиваленцию.
9. Для любого действительного х выполняется неравенство 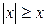 . В символьной форме данное высказывание имеет вид: а)
. В символьной форме данное высказывание имеет вид: а) 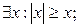 б)
б) 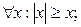 в)
в) 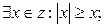 г)
г) 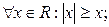
10. С помощью алгоритма Евклида найти наименьший общий делитель чисел 1236 и 2232.
а) 2; б) 6; в) 4; г) 12.
Рекомендуемая литература.
Основная:
1. Нефедов В.Н., Осипова В.А. Курс дискретной математики. - М.: “МАИ”, 1992.
Дополнительная
1. Алферова З.В. Теория алгоритмов. – М.: “Статистика”, 1973.
2. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математике. – М.: “Наука”, 1992
3. Клини С.К. Введение в метаматематику. – М.: “ИЛ”, 1957
4. Столл Р.Р. Множества, логика, аксиоматические теории. – М.: “Просвещение”, 1968.
5. Шафаревич И.Р. Избранные главы алгебры. – М.: “Математическое образование”, 2000.
Словарь основных терминов
Автоморфизм – биективный эндоморфизм, т.е. взаимно однозначное отображение носителя алгебраической структуры на себя, сохраняющие операции сигнатуры.
Алгебраическая структура или алгебра – множество с заданными на нем операциями.
Алгоритм – точное предписание, задающее процесс решения задачи.
Биекция – взаимно однозначное отображение одного множества на другое.
Булева функция – функция, определенная на бинарных наборах заданной длины и принимающая значения из множества {0,1}.
Высказывание – языковое предложение, о котором есть смысл говорить, что оно истинно или ложно.
Гомоморфизм – отображение из одной алгебраической структуры в другую, сохраняющее операции сигнатуры.
Дизъюнктивная нормальная форма (д.н.ф.) – представление булевой функции в виде дизъюнкции элементарных конъюнкций.
Изоморфизм – взаимно однозначное соответствие между носителями алгебраических структур, сохраняющее все операции сигнатуры.
Инъекция – функция, значения которой при различных значениях аргумента различны.
Квантор общности ("x) P(x) – означает, что высказывание P(x) истинно для всех х.
Квантор существования ($х) Р(х) – означает, что существует х, для которого высказывание Р(х) истинно.
Конгруэнтности отношение – отношение эквивалентности на носителе алгебраической структуры, согласованное со всеми операциями сигнатуры в том смысле, что класс эквивалентности, в который попадает результат любой операции сигнатуры, полностью определяется классами, из которых берутся аргументы операции.
Континуум – мощность множества всех действительных чисел, а также отрезка и интервала с несовпадающими концами.
Конъюнктивная нормальная форма (к.н.ф.) – представление булевой функции в виде конъюнкции элементарных дизъюнкций.
Мономорфизм – инъективный гомоморфизм.
Мощность множества – для конечного множества это число элементов, а два бесконечных множества считаются равномощными, если между их элементами может быть установлено взаимно однозначное соответствие.
Предикат – функция, которая при подстановке вместо символов переменных конкретных значений из предметной области превращения в высказывание, т.е. принимает значение «истина» или «ложь».
Сигнатура – множество операций алгебраической структуры.
Счетное множество – множество, имеющее одинаковую мощность с множеством натуральных чисел.
Сюръекция – отображение на всё множество.
Фактор – множество - множество классов эквивалентности.
Фактор – структура – алгебраическая структура, получаемая из данной с помощью отношения конгруэнтности. В качестве её носителя берется фактор – множество, а сигнатура остается прежней.
Частичного порядка отношение – рефлективное, антисимметричное и транзитивное бинарное отношение.
Эквивалентности отношение – рефлексивное, симметричное и транзитивное бинарное отношение. Разбивает множество на непересекающиеся подмножества, называемые классами эквивалентности.
Эндоморфизм – гомоморфное отображение носителя алгебраической структуры на себя.
Эпиморфизм – сюръективный гомоморфизм, т.е. отображение носителя одной алгебраической структуры на весь носитель другой структуры, сохраняющее операции сигнатуры.
Ответы к тестам
I II III IV V
Тест I а) б) в) г) а)
Тест II в) б) б) а) б)
Тест Ш в) в) а) в) б)
Тест IV в) в) в) а) б)
Тест V в) б) б) б) а)
Дата добавления: 2022-02-05; просмотров: 561;











