Вычислительные трудности.

Математическая модель содержит функции, участвующие в процедуре оптимизации. Очевидно, для того чтобы искомый экстремум имел физический смысл, выбранная модель должна адекватно отражать существенные черты реального процесса. Но даже если это требование выполнено, при построении модели встречаются следующие типичные затруднения:

1. Функция цели может быть нечувствительной к изменениям некоторых проектных переменных и поэтому не удается определить четко выраженный экстремум.

2. Функция цели или некоторые из ограничений могут принимать в области поиска решения неограниченные значения; значения частных производных в математической модели также могут стать неограниченными. Особенно подвержены этой опасности модели с полиномами в знаменателе. Так, например, значения функции: 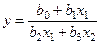; и ее первой частной производной по x₁:

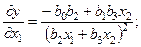
обращаются в бесконечность при b₂ x₁ = - b₃ x₂. Эту трудность можно преодолеть, ограничив области допустимых значений проектных переменных путем введения дополнительных ограничений в задачу, или же изменив формулировку самой математической модели.

3. Переменные могут быть плохо масштабированы. Трудности масштабирования могут возникнуть, например, когда один из членов в выражении для критерия имеет существенно иной порядок величины, чем другой. При этом критерий становится нечувствительным к изменениям значений переменных в меньшем члене. Например, значение целевой функции 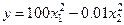будет мало зависеть от изменения x₂, если только значение x₂ не окажется много больше значения x₁. Если x₂ представляет собой величину того же порядка, что и x₁, то либо одну переменную, либо обе переменные можно умножить на масштабные множители, в результате чего оба члена в правой части приведенного выше соотношения окажутся величинами одного и того же порядка. Положим, например,

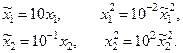
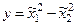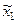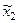Тогда члены в выражении для целевой функции становятся величинами одного порядка. После того как найден экстремум для , можно определить значения x₁ и x₂ по значениям и .Конечно, не всегда удаётся так легко изменить масштаб функций математической модели, как это сделано в рассмотренном примере.

Плохое масштабирование проектных переменных возможно также в случаях, если ограничения и/или целевая функция зависят от них в разной степени. Например, при оптимизации подкреплённых панелей масса панели зависит от толщины обшивки линейно, а от углов ориентации подкрепляющих наборов через sin⁴α и cos⁴α, где α – угол ориентации набора. Изменение на один градус угла ориентации набора приведет к изменению целевой функции порядка 10^-7ρS, а изменение толщины обшивки на один миллиметр – порядка (1 ρS). Здесь ρ – плотность материала панели, а S – её площадь в плане. В этом случае масштабирование переменных требует изобретательности и глубокого понимания механики анизотропных пластин.

4. В плохо построенной математической модели переменные могут оказаться взаимосвязанными. Взаимное влияние переменных можно проиллюстрировать на примере очень простого критерия, в который входит произведение двух параметров: y = 2 x₁ x₂ + 10. Здесь каждая из переменных x₁ и x₂ может принимать различные значения при заданном значении произведения (x₁ x₂). В том случае, когда имеет место взаимное влияние переменных, осуществлять масштабирование гораздо сложнее. Для исключения членов, содержащих произведение двух переменных, квадратичные формы можно привести к каноническому виду. При этом определяются новые координатные оси, называемые главными осями, относительно которых данная поверхность второго порядка симметрична и содержит только аргументы в квадрате. В новой системе координат масштабирование каждого члена значительно проще, чем в исходной системе.

Нелинейные неквадратичные функции можно сделать квадратичными при помощи подходящего преобразования модели или разложения соответствующих функций в ряд Тейлора с сохранением конечного числа членов.

5. В математической модели может оказаться, что некоторые из переменных исключаются путем надлежащего преобразования. Пусть, например,

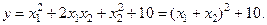
После преобразования 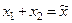, получим 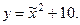Таким образом, вместо двух переменных в выражении для у осталась только одна переменная 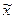, которую и следует варьировать, чтобы найти экстремум функции у.