Геометрическая интерпретация «овражной структуры».

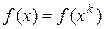– линия с постоянной высотой над уровнем океана. В случае «овражной структуры», как правило, градиент имеет большую длину и направлен почти перпендикулярно к направлению ведущему к оптимальному плану.

Замечание.В случае «овражной структуры» 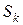надо строить с учётом линий уровня целевой функции, желательно знать кривизну, 2-ую производную.

II этап: решение задачи (4), когда по известному приближению 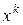построено направление 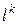выбирается размер окрестности 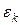, то есть определяется размер шага в этом направлении.

Наиболее распространены 3 способа:

а) наилучший шаг в заданном направлении, решается задача

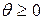(8)

где 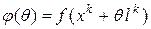. Точное решение задачи (8) выбирается за .

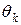Определение.Метод 1-го порядка, в котором шаг выбирается в виде (7), а направление наилучшим называется методом наискорейшего спуска.

б) 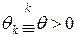, где – малое число, при этом способе на всех итерациях шаг выбирается одинаковым.

Замечание.Если шаг выбрать достаточно большим, то даже если направление позволяет уменьшить целевую функцию, с этим шагом функция возрастёт. (Перейдём на противоположную сторону оврага и более высокую.)

в) метод последовательного дробления.

При таком выборе шага задача (8) решается подбором. Выбираем сначала 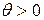и сравниваем значения 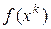и 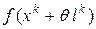. Если между числами знак 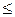, то шаг большой (целевая функция увеличивается) и уменьшают в несколько раз (10). Поле чего повторяем сравнение. Если знак 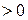, то шаг подходит, но и в этом случае его можно улучшить (в несколько раз увеличить или уменьшить ). Существуют специальные схемы подбора шага итераций.