Задача распределения ресурса
Постановка задачи. Имеется некоторый однотипный ресурс (нефть, зерно) в объёме 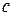 . Этот ресурс можно использовать в
. Этот ресурс можно использовать в 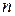 технологических процессах и причём известно, что если
технологических процессах и причём известно, что если 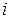 -му процессу выделить ресурс в объёме
-му процессу выделить ресурс в объёме 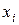 , то получим прибыль
, то получим прибыль 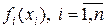 . Требуется распределить ресурс между процессами таким образом, чтобы суммарная прибыль была максимальной.
. Требуется распределить ресурс между процессами таким образом, чтобы суммарная прибыль была максимальной.
Математическая модель. Целевая функция (суммарная прибыль) будет
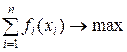 (1)
(1)
Ограничения:
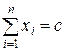 (2)
(2)
(В (2) можно использовать и неравенство 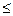 , однако, как правило, ресурс используется полностью.)
, однако, как правило, ресурс используется полностью.)
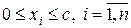 (3)
(3)
(2)-(3)– прямые ограничения. (1)-(3) – математическая модель задачи. Задача (1)-(3) относится к задачам сепарабельного программирования, так как и целевая функция и все ограничения в ней задаются с помощью сепарабельных функций.
Определение.Функция 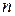 переменных называется сепарабельной, если она представима в виде линейной комбинации функций одной переменной.
переменных называется сепарабельной, если она представима в виде линейной комбинации функций одной переменной.
К таким задачам, в частности, всегда применим метод динамического программирования.Общая схема метода динамического программирования
Метод, как правило, включает 3 этапа:
I этап: инвариантное погружение. На этом этапе исходная задача погружается в семейство подобных ей задач, зависящие от 2-х параметров, один из которых обычно динамический(время, этап). Оптимальное значение целевой функции отдельной задачи этого семейства (при фиксированных значениях параметров) называется функцией Беллмана.
II этап: строится уравнение Беллмана для этой функции. На этом этапе используется принцип оптимальности Беллмана, который формулируется следующим образом: любая часть оптимального решения (которая представляет из себя некоторую траекторию во времени или развивается поэтапно) начинающаяся с любого момента является сама оптимальной относительно достигнутого состояния.
Пример.
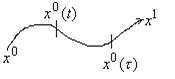
Пусть имеется оптимальная траектория  , связывающая две точки
, связывающая две точки 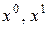 , для
, для 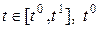 – начальный момент,
– начальный момент, 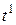 – конечный момент;
– конечный момент; 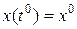 – начальное состояние,
– начальное состояние, 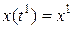 – конечное состояние. Эта траектория оптимальная в связи с некоторой целевой функцией. Предположим, что в некоторый момент
– конечное состояние. Эта траектория оптимальная в связи с некоторой целевой функцией. Предположим, что в некоторый момент 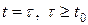 мы достигаем состояния
мы достигаем состояния 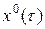 и пытаемся из этого состояния и из этого момента достигнуть
и пытаемся из этого состояния и из этого момента достигнуть 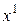 оптимальным образом. Тогда принцип оптимальности Беллмана утверждает, что решением этой задачи будет соответствующий (оставшийся) кусок траектории
оптимальным образом. Тогда принцип оптимальности Беллмана утверждает, что решением этой задачи будет соответствующий (оставшийся) кусок траектории 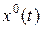 .
.
III этап: заключается в решении уравнения Беллмана (при всех значениях параметров определяется функцией Беллмана) и построению по этому решению оптимального плана исходной задачи.
Инвариантное погружение для задачи (1)-(3)
Рассмотрим в (1)-(3) первых 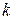 технологических процесса
технологических процесса 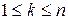 и выделим для них ресурс в объёме
и выделим для них ресурс в объёме 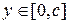 и будем этот ресурс для этих процессов распределять оптимально, тогда приходим к задаче:
и будем этот ресурс для этих процессов распределять оптимально, тогда приходим к задаче:
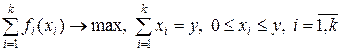 (4)
(4)
это и есть искомое семейство. Если в (4) положить 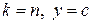 , то придём к исходной задаче (1)-(3). То есть погружение осуществлено корректно. Оптимум целевой функции семейства (4) при фиксированных
, то придём к исходной задаче (1)-(3). То есть погружение осуществлено корректно. Оптимум целевой функции семейства (4) при фиксированных 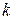 и
и 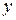 , то есть максимальную прибыль, которую можно получить, если распределить среди первых
, то есть максимальную прибыль, которую можно получить, если распределить среди первых 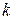 процессов ресурс
процессов ресурс 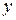 называется функцией Беллмана и обозначается
называется функцией Беллмана и обозначается 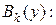
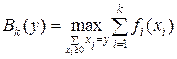 .
.
Дата добавления: 2021-07-22; просмотров: 534;











