Решение уравнения (6)-(7)

Математическая модель. Целевая функция (суммарная прибыль) будет

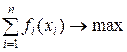(1)

Ограничения:

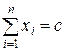(2)

(В (2) можно использовать и неравенство 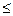, однако, как правило, ресурс используется полностью.)

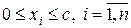(3)

Рассмотрим в (1)-(3) первых 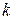технологических процесса 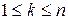и выделим для них ресурс в объёме 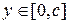и будем этот ресурс для этих процессов распределять оптимально, тогда приходим к задаче:

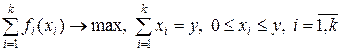(4)

Уравнение (6) будем решать последовательно, положим в (6) 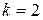, тогда получим 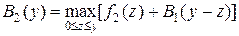. Справа под максимумом стоит известная функция, решая задачу максимизации, найдём .

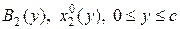На 2-ом шаге полагаем в (6) 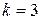, аналогично находим 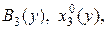и так далее. Пройдя последовательно 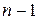шаг, мы построим полное решение уравнения Беллмана: .

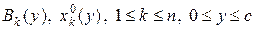Приступаем к построению оптимального плана задачи (1)-(3). Полагаем в функции Беллмана 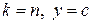тогда, очевидно, 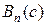будет искомая максимальная прибыль. Одновременно мы найдём 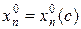. Эта оптимальная компонента для 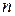-го ресурса, тогда для процессов 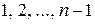остаток ресурса будет 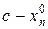и найдём, что 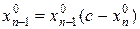и так далее. Для любого 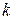: 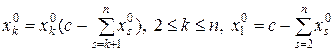. Задача решена полностью.

Метод динамического программирования имеет свои преимущества и недостатки.

Преимущества:

1) задача оптимизации с 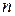переменными сводится к 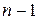задачи одномерной оптимизации.

2) результатом метода динамического программирования является всегда оптимальный план (глобально), а не локально оптимальные планы как в большинстве других планов.

3) результаты решённой задачи оптимизации можно использовать в случае изменения параметров 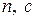(задачу не надо пересчитывать заново).

4) как правило, задача одномерной оптимизации решается методом поиска, поэтому метод динамического программирования может использоваться для задачи оптимизации, в которых функции не являются дифференциальными, непрерывными, аналитическими.

Недостаток динамического программирования – «проклятие размерности». Дело в том, что при решении задач на ЭВМ требуется хранить в памяти значение функции Беллмана, то есть запоминать функции. Количество запоминаемой информации растёт лавинообразно с ростом размерности задачи (если распределяется не один ресурс, а 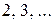). Разработаны специальные подходы, которые позволяют смягчить этот недостаток.