Градиентные методы. Выбор шага
Задачу (4) будем решать в 2 этапа:
I этап: построение направлений итерации. Полагаем в задаче (4) по известному 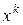 :
: 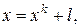 где
где 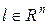 , в результате приходим к задаче:
, в результате приходим к задаче:
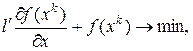
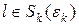 (5)
(5)
где 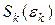 – некоторая окрестность начала координат в
– некоторая окрестность начала координат в 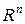 размерами
размерами 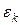 . В результате решения задачи (5) получаем некоторый вектор
. В результате решения задачи (5) получаем некоторый вектор 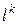 . Он выбирается за направление на
. Он выбирается за направление на 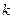 -ой итерации. При выборе направления его размеры не важны, поэтому
-ой итерации. При выборе направления его размеры не важны, поэтому 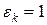 , то есть
, то есть 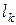 имеет единичную длину.
имеет единичную длину.
Константа 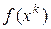 в (5) также на направление не влияет и её отбрасывают. Таким образом, для нахождения
в (5) также на направление не влияет и её отбрасывают. Таким образом, для нахождения 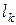 решается задача:
решается задача:
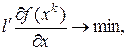
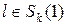 (5*)
(5*)
Пример. Рассмотрим в (5) случай, когда окрестность есть единичный шар, то есть будем решать задачу:
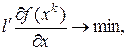
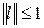 (6)
(6)
Решаем задачу (6) геометрически: 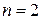 .
.
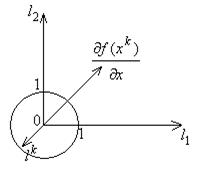
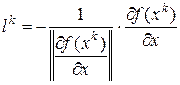 – оптимальный план задачи (6).
– оптимальный план задачи (6).
Поскольку размеры направления нас не интересуют, то в методах 1-го порядка используют направление
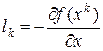 – направление антиградиента (7)
– направление антиградиента (7)
Методы 1-го порядка с таким направлением называются градиентными. Градиентные методы – наиболее популярные методы 1-го порядка. Если выбрать подходящий шаг, то они всегда позволяют уменьшить целевую функцию. Однако существуют задачи (1) с так называемой «овражной структурой», для которых градиентные методы плохо сходятся и надо направление выбирать другим (по-другому выбирать окрестность 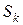 ).
).
Дата добавления: 2021-07-22; просмотров: 484;











