Метод случайного поиска

В этом методе на 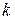-ой итерации по известному приближению 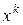в качестве 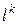выбирается некоторый случайный вектор единичной длины, 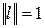. При этом используются механизмы теории вероятности (датчик случайных чисел). После того, как направление 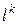выбрано, проверяется, является ли оно подходящим. Если выполняется 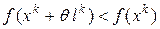, для некоторого 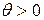малого, то 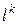выбирается в качестве направлений итерации и осуществляется итерация, шаг выбирают по 3-ему способу. Если 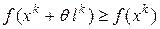, то шаг изменяется на противоположный либо выбирается по-новому.

Замечание. Не всегда противоположное направление оказывается подходящим. (Если в качестве случайного направления выбрано касательное, то и противоположное не будет подходящим.)

Один из самых популярных методов 1-го порядка, который по сходимости близок к методу 2-го порядка – метод сопряжённого градиента.

При выборе метода для решения конкретной задачи надо учитывать всю информацию, тип целевой функции, её гладкость, форму поверхности уровня, кривизну и так далее.

Общая рекомендация: первые итерации лучше проводить грубыми методами (метод поиска), затем переходить к методу 1-го порядка, а затем в малых окрестностях решения можно использовать метод Ньютона (так как там обычно выполняется неравенство (12)).

10.МЕТОДЫ УСЛОВНОЙ МИНИМИЗАЦИИ. Случай линейных ограничений

Пусть дана задача:

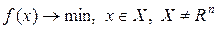(1)

Пусть требуется решить задачу:

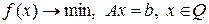(2)

где 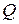– множество простой структуры, которое задаётся с помощью ограничений на одну переменную вида .

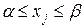В методах 1-го порядка на 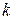-ой итерации по известному 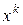решается задача

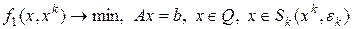(3)

Как правило, окрестность 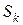в (3) формируется с помощью линейных ограничений. Поэтому задача (3) представляет из себя задачу линейного программирования, её решение принимается за .

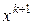Если в задаче (3) вначале искать направление итерации и положить 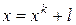, то в результате придём к задаче

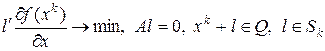(4)

Решение этой задачи принимается за 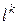. Задача (4), как правило, линейная задача. После определения направления итерации шаг выбирают одним из описанных 3-х способов.

Пример 1. Положим 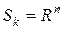в (4), тогда получим задачу:

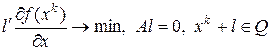(5)

Решение этой задачи называется направлением условного градиента. Это направление даёт наибольшую проекцию на антиградиент и не выводит за пределы .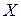

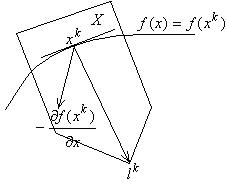
Пример 2. Положим 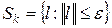, тогда получим задачу:

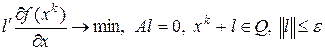(6)

а) 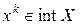. В этом случае 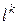совпадает по направлению с антиградиентом и имеет длину 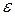, (то есть в этом случае используется классический градиентный метод).

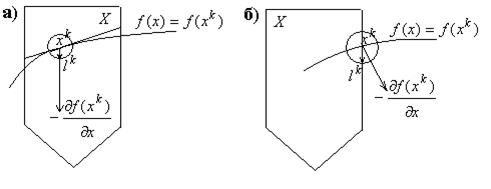
б) 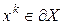, значит, антиградиент проектируется на 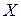и имеет длину .

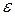Если в (3) вместо 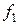использовать 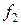, то для задачи (2) получаем метод Ньютона.