Геометрическая вероятность

Одним из недостатков классического определения вероятности является конечность группы равновероятностных событий. Поэтому встала задача построения понятия вероятности для случаев, когда мыслится бесконечное, континуальное множество исходов. При этом по-прежнему основную роль играло понятие «равновозможности» событий.

Общая задача, которая ставилась и привела к расширению понятия вероятности, может быть сформулирована следующим образом:

Рассмотрим некоторую область G спрямляемую, квадрируемую или кубируемую, соответственно на плоскости или в пространстве. И другую область 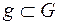, имеющую соответствующую меру. Будем считать, что мера границы областей равна нулю. В область G наудачу бросается точка. Какова вероятность, что она попадет в область g?

Здесь выражение «точка бросается наудачу в область G» имеет следующий смысл:

Если разделить область G на конечное число равновеликих частей g_i (i = 1,2,…,n), то события, состоящие в попадании точки в любую часть g_i, считаются равновозможными. Тогда можно считать, что вероятность попадания в какую-либо часть g области G пропорциональна мере этой части и не зависит от ее формы и расположения в области G:

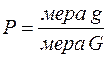
Пример. Задача о встрече: Два лица А и В условились встретиться в определенном месте, между 12 и 13 часами. Пришедший первым ждет в течение 20 минут другого, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них в течении указанного часа может произойти наудачу и моменты прихода независимы?

Решение: Пусть x – момент прихода лица А, y – момент прихода лица В. Обозначим через G множество точек плоскости XOY

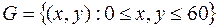
Тогда условие встречи можно выразить неравенством .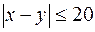

Через область g обозначим подмножество

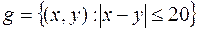
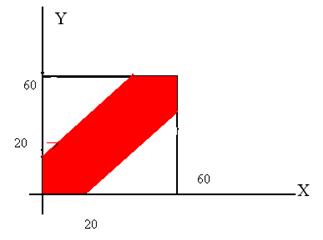
На рисунке область g выделена цветом. Нетрудно вычислить:

.

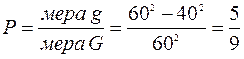Теория геометрической вероятности неоднократно подвергалась критике за произвольность определения вероятности событий. При этом многие авторы приходили к убеждению, что для бесконечного множества исходов нельзя дать объективного, не зависящего от способа решения, определения вероятности. В качестве примера приведем одну задачу известного французского математика Жозефа Бертрана, которая получила название

Парадокс Бертрана

Задача. В круге радиуса R наудачу берется хорда. Чему равна вероятность того, что ее длина окажется больше стороны правильного, вписанного в этот круг треугольника?

Решение 1. Зададим направление хорд (в силу симметрии круга, это не влияет на решение). Проведем диаметр АВ=d=2R перпендикулярный выбранному направлению.

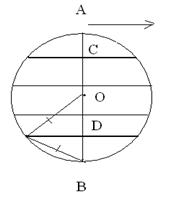
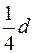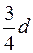Очевидно, что только хорды, пересекающие диаметр на отрезке [C,D] от до , будут удовлетворять условию задачи. Тогда

.

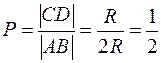Решение 2. Закрепим один из концов хорды на окружности. Касательная к окружности и две стороны правильного треугольника с вершиной в точке касания, образуют углы по 60^о.

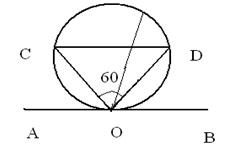
Хорды, попадающие в средний угол, будут превосходить стороны треугольника COD. Тогда

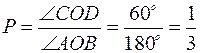
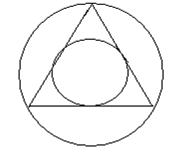
Решение 3. Чтобы определить положение хорды, достаточно задать ее середину. Хорды, середины которых лежат внутри круга, концентрического с данным кругом, с половинным радиусом, будут удовлетворять условию задачи.

Тогда искомая вероятность равна

.

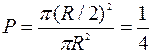Причина неоднозначности решения заключается в том, что за решение одной и той же задачи, пользуясь тем, что в условии не определено понятие проведения хорды наудачу, выдаются решения трех различных задач.

В первом решении вдоль одного из диаметров заставляют «катиться» круглый цилиндрический стержень. Множество возможных мест остановок стержня есть множество точек диметра АВ. Равновероятностными считаются события, состоящие в то, что остановка произойдет на отрезке длины h, где бы он не находился внутри отрезка АВ.

Во втором решении стержень закреплен в одной из точек окружности и его заставляют «качаться» в пределах 180^о. При этом предполагается, что остановка стержня внутри дуги длиной h зависит только от длины h, но не от ее положения на окружности, т.е. равновероятностными считаются остановки на любом участке окружности длины h.

В третьем решении внутрь круга наудачу «бросается» точка и определяется вероятность ее попадания внутрь некоторого меньшего круга. Здесь равновероятностными считаются попадания точки в любые части исходного круга, имеющие одинаковые площади.

Различие постановок задач очевидно и заключается в неоднозначности понятия проведении хорды наудачу.