Составление уравнения для функции Беллмана

Математическая модель. Целевая функция (суммарная прибыль) будет

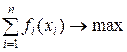(1)

Ограничения:

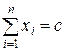(2)

(В (2) можно использовать и неравенство 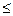, однако, как правило, ресурс используется полностью.)

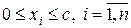(3)

Рассмотрим в (1)-(3) первых 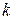технологических процесса 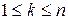и выделим для них ресурс в объёме 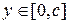и будем этот ресурс для этих процессов распределять оптимально, тогда приходим к задаче:

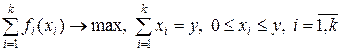(4)

Зафиксируем в (4) параметры 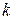и 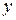и задачу (4) будем решать следующим образом: последнему 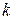-му процессу выделим ресурс в объёме 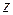и получим прибыль 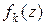, тогда процессам 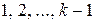останется ресурс в объёме 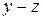. Предположим, что распределение этого остатка осуществляется оптимальным образом, тогда получим прибыль 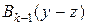. В результате такого подхода решение задачи (4) суммарная прибыль: .

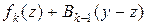Будем изменяться 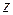и искать такое значение для него, чтобы получаемая прибыль была наибольшей, то есть будем решать задачу:

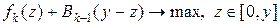(5)

Согласно принципу оптимальности Беллмана оптимальное значение целевой функции задачи (5) равно 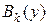. То есть выполняется отношение:

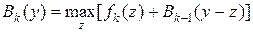(6)

(6) – искомое уравнение Беллмана. Решая задачу (5), мы найдём для неё оптимальный план 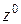. Это, очевидно, будет оптимальное количество ресурса, которое выделяется 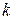-му ресурсу в задаче (4). То есть оптимальное количество ресурса, которое получает 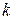-ый процесс при наилучшем распределении ресурса в объёме 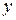ля первых 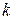процессов: 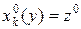. Уравнение (6) по динамическому параметру 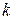рекуррентно, поэтому для того, чтобы его решить нужно задать для (6) начальные условия. Они получаются, если положить в (4) 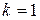, тогда приходим к задаче: 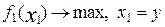. Эта задача тривиальна, у неё единственный план 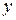и оптимальное значение целевой функции тогда будет:

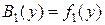(7)