Арифметическая и геометрическая прогрессии. Арифметическая прогрессия
Арифметической прогрессией называется такая последовательность чисел, каждый член которой, начиная со второго равен предыдущему, сложенному с некоторым числом. Это число называется разностью прогрессии. Таким образом,
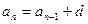 ,
,
где 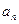 и
и 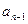 соответственно n-й и n+1-й члены прогрессии, d – разность прогрессии.
соответственно n-й и n+1-й члены прогрессии, d – разность прогрессии.
Примеры: 1) Последовательность всех натуральных чисел 1, 2, 3, 4, 5, … есть арифметическая прогрессия с разностью d =1 и первым членом 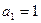 ;
;
2) Последовательность 7, 3, -1, -5, -9, -13, … есть арифметическая прогрессия с разностью d = -4 и первым членом 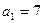 .
.
Для вычисления 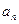 можно использовать более удобную формулу
можно использовать более удобную формулу
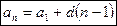 .
.
Сумма первых n членов арифметической прогрессии вычисляется по формуле
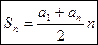 или
или 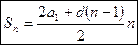 .
.
Пример 1. В арифметической прогрессии 8, 12, 16, 20, 24, … первый член 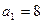 , разность d = 4, найти двадцатый член прогрессии и сумму первых двадцати членов.
, разность d = 4, найти двадцатый член прогрессии и сумму первых двадцати членов.
Решение. Двадцатый член прогрессии равен 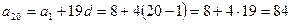 .
.
Сумма первых двадцати членов равна
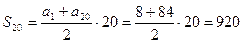 .
.
Ответ: 84; 920.
Пример 2. В арифметической прогрессии 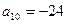 и
и 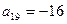 . Найдите количество неотрицательных членов прогрессии, каждый из которых меньше 42.
. Найдите количество неотрицательных членов прогрессии, каждый из которых меньше 42.
Решение. Так как 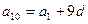 ,
, 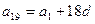 , то значения
, то значения 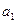 и d можно найти, решив систему:
и d можно найти, решив систему:
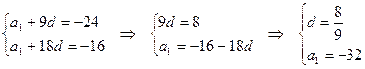
По условию 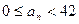 , т.е.
, т.е. 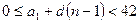 . Подставляем в формулу значения
. Подставляем в формулу значения 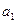 и d, затем выражаем из полученного неравенства значение n:
и d, затем выражаем из полученного неравенства значение n:
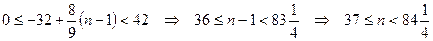 .
.
Количество целых чисел, принадлежащих данному промежутку, равно 48. Таким образом, количество членов прогрессии, удовлетворяющих условию задачи, равно 48.
Ответ: 48.
Пример 3. Найдите сумму всех целых чисел k, каждое из которых делится без остатка на 26 и удовлетворяет условию -339<k <443.
Решение. Первым числом, которое удовлетворяет этим условиям, является -338, а последним 442. Таким образом, требуется найти сумму k членов арифметической прогрессии, для которой 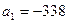 ,
, 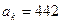 , d = 26. Найдём k, используя формулу
, d = 26. Найдём k, используя формулу 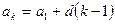 . Получаем
. Получаем 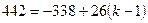 , отсюда k = 31. Тогда
, отсюда k = 31. Тогда 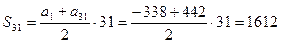 .
.
Ответ: 1612.
Признак арифметической прогрессии: каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое соседних с ним членов:
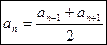 .
.
Дата добавления: 2020-05-20; просмотров: 842;











