Геометрическая анизотропия

На рисунке 3.4. изображены примеры геометрической анизотропии. На левом рисунке вариограммы имеют одинаковый порог в обеих направлениях, но зоны влияния различны, в то время, как на правом рисунке обе функции линейны, но имеют разные углы наклона.

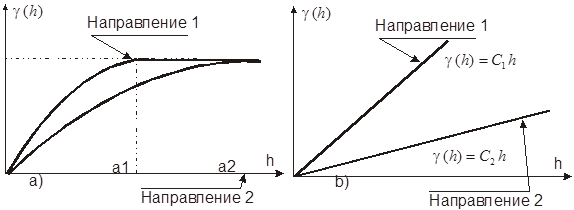
Рис 3.4. Эллиптическая или геометрическая анизотропия

Мы можем нарисовать диаграмму, показывающую зависимость зоны влияния или угла наклона в зависимости от направления. (Рис. 3.5.). Если кривая является эллипсом (в 2-х мерном пространстве), то анизотропия называется геометрической (или эллиптической). В этих случаях простейшими изменениями координат эллипс преобразуется в окружность, и анизотропия устраняется.

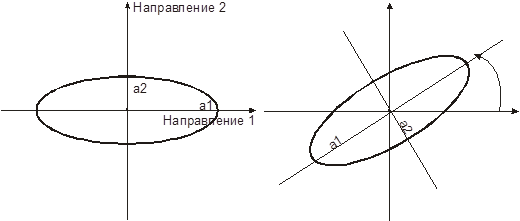
Рис 3.5. Эллипсы, показывающие главные оси эллипса в случае геометрической анизотропии

Это преобразование особенно просто, когда главная ось эллипса совпадает с координатными осями, как показано на Рис. 3.5. (a). Затем если уравнение вариограммы в направлении 1 есть 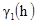, то общая вариограмма после исправления анизотропии имеет следующий вид:

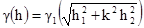[3.4]

где h₁ и h₂ – два компонента h, и k – отношение анизотропии, определенное, как:

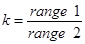или 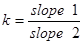(range – зона влияния , slope – угол наклона ) [3.5]

При первом вычислении вариограммы, важно исследовать по крайней мере четыре направления. Если вариограмма вычисляется только в двух перпендикулярных направлениях, то анизотропию возможно потерять полностью. Это случается, например, когда главные оси эллипса анизотропии повернуты относительно направлений, в которых рассчитываются вариограммы, на 45 градусов, как показано на Рис. 3.5.b.