Анализ и интерпретация результатов компьютерного моделирования

Возможность фиксации при компьютерномэкспериментальном моделировании системы значений переменных или параметров и их статистическая обработка для получения интересующих исследователя характеристик по­зволяют провести объективный анализ связей между этими вели­чинами. Для решения этой задачи существуют различные методы, зависящие от целей исследования и вида получаемых при моделировании характеристик. Рассмотрим особенности использования методов корреляционного, регрессионного и дисперсионного анализа для результатов моделирования систем [5].

10.4.1. Корреляционный анализ результатов моделирования

С помощью корреляционного анализа можно установить, насколь­ко тесна связь между двумя или более случайными величинами, наблюдаемыми и фиксируемыми при моделировании конкретной системы. Корреляционный анализ результатов моделирования сводится к оценке разброса значений относительно среднего значе­ния 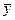, т. е. к оценке силы корреляционной связи. Существование этих связей и их силу можно для схемы корреляционного анали­за у=М[η/ξ=х] выразить при наличии линейной связи между ис­следуемыми величинами и нормальности их совместного распределения с помощью коэффициента корреляции

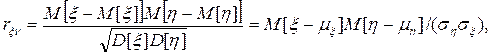
т. е. второй смешанный центральный момент делится на произведе­ние средних квадратичных отклонений, чтобы получить безразмерную величину, инвариантную относительно единиц измерения рассмат­риваемых случайных переменных.

Пример. Пусть результаты моделирования получены при N реализациях, а коэффициент корреляции

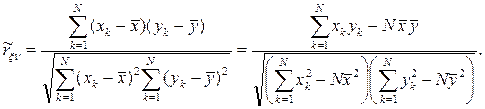
Данное соотношение требует минимальных затрат компьютерной памяти на обработку результатов моделирования. Получаемый при этом коэффици­ент корреляции |r_ξη|≤1. При сделанных предположениях r_ξη=0 свидетельствует о взаимной независимости случайных переменных ξ и η, исследуемых при моделиро­вании (рис. 10.1).

Рис. 10.1. Случай отсутствия корреляции переменных x и y

При r_ξη =1 имеет место функциональная, т. е. не стохастическая, линейная зависимость вида у=b₀+b₁х, причем если r_ξη > 0, то говорят о положитель­ной корреляции, т. е. большие значения одной случайной величины соответствуют большим значениям другой (рис. 10.2).

Рис. 10.2. Случай функциональной линейной зависимости переменных x и y

Случай 0 <r_ξη < 1 соответствует либо наличию линейной корреляции с рассеянием (рис. 10.3), либо наличию нелинейной корреляции результатов моделирования (рис. 10.4).

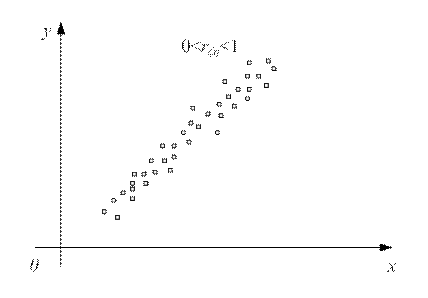
Рис. 10.3. Случай линейной корреляции переменных x и y с рассеянием

Для того чтобы оценить точность полученной при обработке результатов моделирования системы оценки, целесообразно ввести в рассмотрение коэффициент w=1n[(1+r_ξη)/(1–r_ξη)]/2, при­чем w приближенно подчиняется гауссовскому распределению со средним значением и дисперсией:

μ_w=ln[(1+r_ξη)/(1–r_ξη)]/2;

.

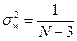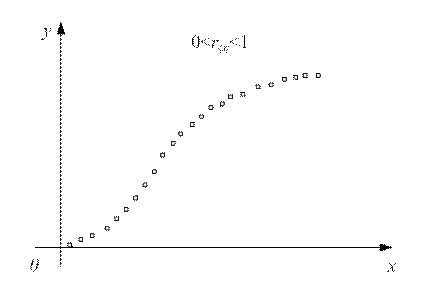
Рис. 10.4. Случай нелинейной корреляции переменных x и y

Из-за влияния числа реализаций при моделировании N на оценку коэффициента корреляции необходимо убедиться в том, что 0≤r_ξη≤1 действительно отражает наличие статистически значимой корреляционной зависимости между исследуемыми переменными модели. Это можно сделать проверкой гипотезы Н₀: r_ξη=0. Если гипотеза Н₀ при анализе отвергается, то корреляционную зависимость признают статистически значимой. Очевидно, что выбороч­ное распределение введенного в рассмотрение коэффициента w при r_ξη=0 является нормальным с нулевым средним μ_w=0 и дисперсией 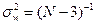. Следовательно, область принятия гипотезы Н₀ опре­деляется неравенством

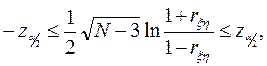
где z_α/2 подчиняется нормированному гауссовскому распределению. Если r_ξη лежит вне приведенного интервала, то это означает наличие корреляционной зависимости между переменными модели на уров­не значимости γ.

При анализе результатов моделирования системы важно отметить то обстоятельство, что даже если удалось установить тесную зависимость между двумя переменными, то отсюда еще непосредственно не следует их причинно-следственная взаимообуслов­ленность. Возможна ситуация, когда случайные величины ξ и η стохастически зависимы, хотя причинно они являются для системы независимы­ми. При статистическом моделировании наличие такой зависимо­сти может иметь место, например, из-за коррелированности последовательностей псевдослучайных чисел, используемых для имита­ции событий, положенных в основу вычисления значений х и у.

Таким образом, корреляционный анализ устанавливает связь между исследуемыми случайными переменными компьютерной модели и оценивает тесноту этой связи. Однако в дополнение к этому желательно располагать моделью зависимости, полученной после обработки результатов моделирования.