Общая схема методов 2-го порядка. Метод Ньютона

Рассмотрим задачу:

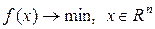(1)

В методах 2-го порядка на 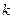-ой итерации по известному приближению 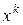решается задача

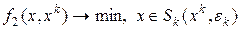(9)

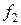– квадратичная аппроксимация. Если окрестность строится с помощью линейных ограничений, то (9) – задача квадратичного программирования, её решение – .

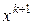Различные способы задания окрестности 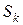задают различные методы. Будем решать (9) в 2 этапа:

I этап: 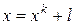, 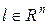. Тогда придём к задаче:

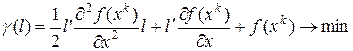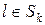, (10)

Решение этой задачи принимается за 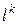– направление итерации. Шаг выбирается одним из 3-х способов (из 3.3)

Пример. Пусть в задаче (1) выполняется условие

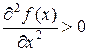(11)

то есть функция является строго выпуклой.

Замечание. Условие (11) может выполняться в некоторой окрестности решения задачи, тогда и функция 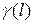строго выпукла 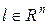. Задача (10) имеет решение, даже если положить 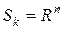и будет находиться в стационарной точке .

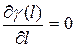Положим в (10) 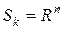и составим уравнение стационарности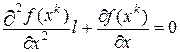

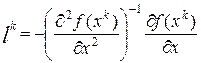(12)

Направление итерации, которое выбирается по формуле (12) называется направлением Ньютона, а методы, основанные на таком либо подобном направлении, называется ньютоновскими. В частности. Если положить 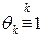, то получим классический метод Ньютона.

Геометрическая интерпретация направлений Ньютона: в 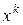к линии уровня 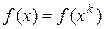строим касательный эллипс: 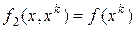. Направление Ньютона ведёт в центр эллипса (матрица 2-го порядка (12) как бы поворачивает антиградиент в сторону оптимального плана и нормализует его длину (формирует шаг)). Поэтому методы 2-го порядка более точные и быстрее сходятся.