Методы условной минимизации. Метод штрафных функций

Пусть дана задача:

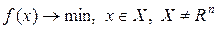(1)

Определение. Пусть дано некоторое 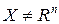. Тогда штрафной функцией этого множества называют функцию со следующими свойствами:

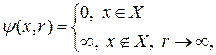
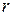– некоторый неотрицательный скалярный параметр, с ростом которого неограниченно растёт функция .

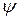Штрафную функцию можно интерпретировать как штраф за отклонение от 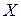, а 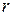характеризует относительную величину этого штрафа.

Пример 1. 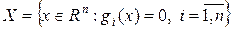– множество планов задачи с ограничениями равенствами, то можно положить .

Пример 2. 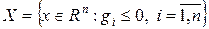– множество планов задачи с неравенствами, тогда .

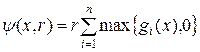Существуют специальные способы подбора штрафных функций для различных типов множеств. Штрафные функции различаются по порядку роста. Существуют штрафные функции, которые имеют полиномиальный рост, экспоненциальный рост, логарифмический рост в зависимости от отклонения от X.

Пусть дана задача (1) и для 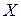построена штрафная функция, тогда метод штрафных функций заключается в решении вместо задачи (1), задачи на безусловный минимум

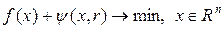(7)

В задаче (7) возможны 2 подхода:

1 составляем для целевой функции условие стационарности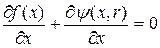

Находим стационарную точку 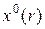, затем находим точку

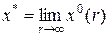(8)

Иногда, таким образом, удаётся построить в точности оптимальный план.

2 в других случаях задача (7) решается приближёнными методами.